 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Holes



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We had a few solutions sent in for this challenge. I think that maybe there were other pupils who got so far, on their own or with the teacher, and decided it was not worth sending in. We would like to reassure you that all journeys in the solving of challenges - however far you get - we welcome!
Here is the excellent result that we received from class $5$A at St. Christopher's School in Penang, Malaysia.
Well Done !
From Jenthghe and Olivia we received.
For this problem we used a trial and error method!
For solid cube number $1$ we did, $3$x$3$x$3$=$27$
For frame cube number $1$ we did $3$x$3$x$3$=$27-7=20$ we took away $7$ because there was seven holes in the cube.
We did the same for solid and frame cube number $2$ but this time we found that we had to do $4$x$4$x$4$=$64$ (for the solid cube), then find what the frame cube had which was $4$x$4$x$4$=$64-24=40$ (for the frame) we took $24$ away because that was how many holes were in the cube.
For solid and frame number $3$ we did $5$x$5$x$5$=$125$ (for the solid cube) and for the frame we did $5$x$5$x$5$=$125-65=60$. we took away $65$ because there were $65$ cubes missing.
This was a good start to this challenge but a closer look at the frame cubes would be necessary. Then you might see that the $24$ you take away from $64$ cubes for the second cube only takes account of the $4$ cubes on each face that were removed. There was also some cubes removed from the centre of the solid cube and they would form a $2$ by $2$ by $2$ cube. This would mean a total of $32$ cubes altogether.
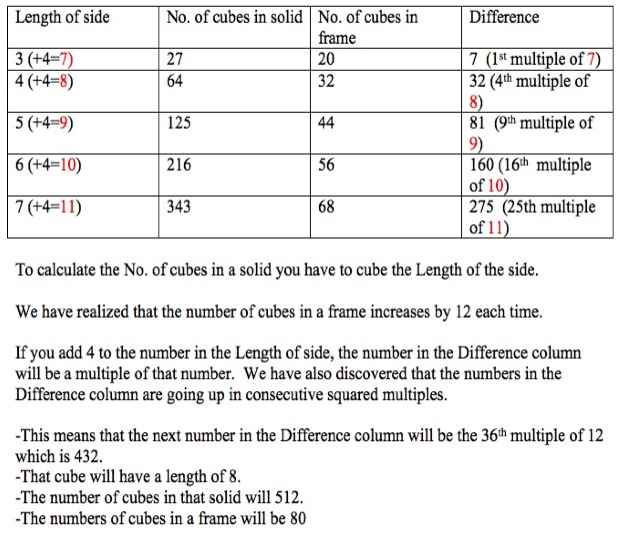
Shriya from the International School Frankfurt in Germany sent in this:I used Lego blocks to build the cube frame.For the 4×4×4 cube, I got 32 cubes with holes and 64 without. For the 5×5×5 cube, I got 44 cubes with holes and 125 without. For the 6×6×6 cube, I got 56 cubes with holes and 216 without. After this, I found out the pattern. There was a difference of 12.
12 × (n - 3) + 20. I confirmed this by building a 7×7×7 cube and my guess was correct. I got 68 cubes with holes and 343 without. Now, with the formula above, I can predict how many cubes I will need to make a cube frame.
Thank you for these solutions.
You may also like
Cereal Packets
How can you put five cereal packets together to make different shapes if you must put them face-to-face?