My friend has two function machines. The first, called RECIPROCAL, takes as an input any function $f(x)$ and returns another function $1/f(x)$. The second, called PRODUCT, takes two functions $f(x)$ and $g(x)$ and returns a new function which is their product $f(x)g(x)$.

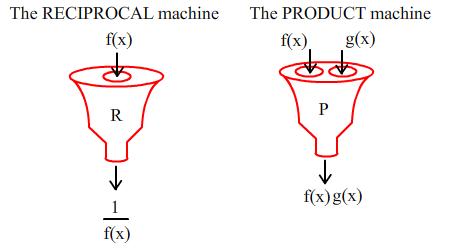
I start off with the function $f(x)=x$. Which functions can I make using the function machines RECIPROCAL and PRODUCT? Can you describe an entire theoretical set of such outputs? Prove your assertions. (Note that I have several copies of this function to hand). Are there any other starting functions which yield the same set of outputs? What sets of outputs will I get by starting with different initial functions?

I have two operator machines. The first, called DIFF, takes any input function and returns another function which is its derivative. (If the derivative function does not exist, then DIFF returns the original function). The second, called INT, takes any input function and returns the implicit integral (i.e. no constant of integration) of the original function (if this integral does not exist then INT returns the original function).



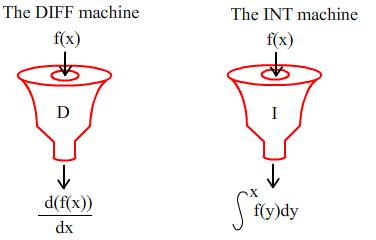
If I again start off with the function $f(x) = x$, what set of outputs can I make using DIFF and INT? Are there any other starting functions which yield the same set of outputs? What sets of outputs will I get by starting with different initial functions?

Can you find any initial functions which yield a finite set of possibilities under RECIPROCAL and PRODUCT or under DIFF and INT?

What happens if you begin with $f(x) = x$ and use any combination of RECIPROCAL and DIFF?

Explore the possibilities when you can use different combinations of RECIPROCAL, PRODUCT, DIFF and INT for various choices of initial function. Can you find any interesting sets of outcomes?

See also the problem Calculus Countdown