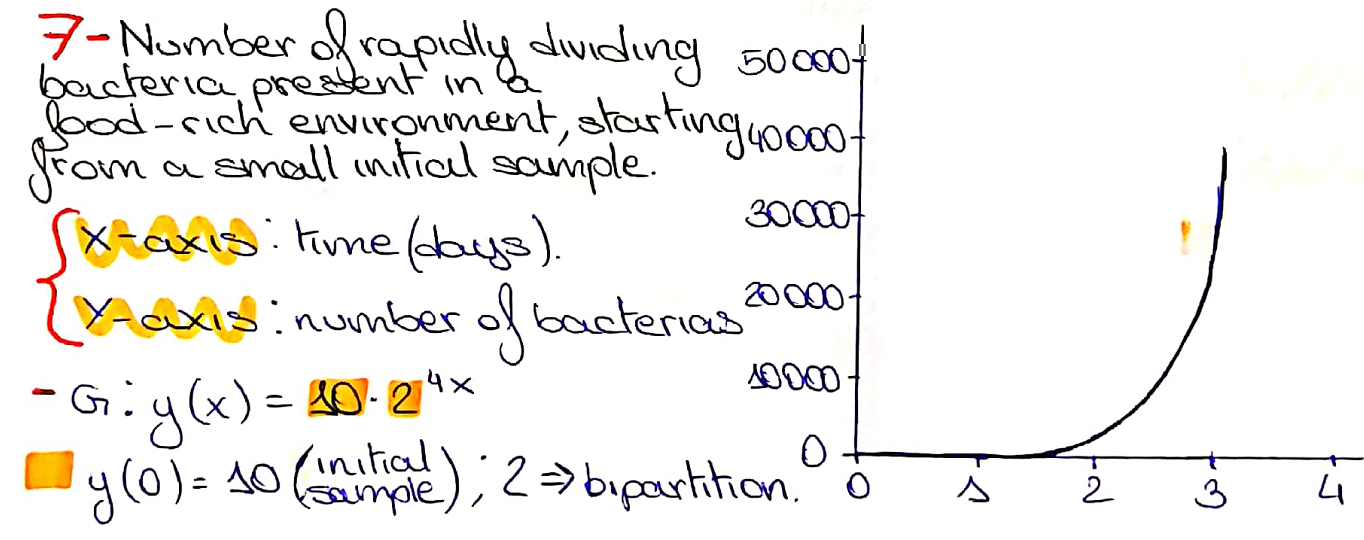Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Whose Line Graph Is it Anyway?



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
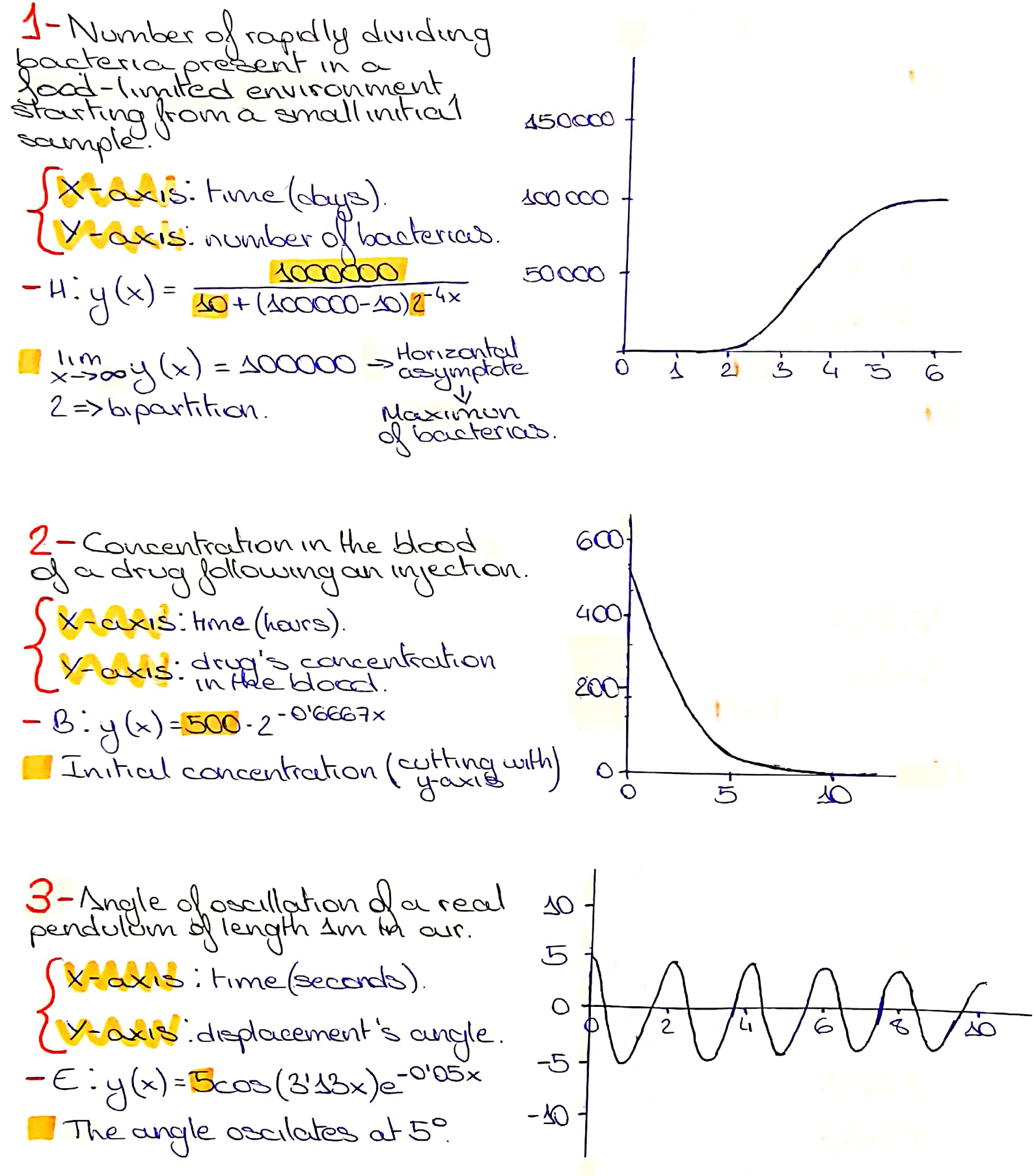
Raquel from IES Maximo Laguna in Spain and Rishik K both chose the same graphs for the processes numbered 1 to 3. Below is Raquel's work, which also shows equations and reasons for the choices of constants (click on the image to open a larger version).
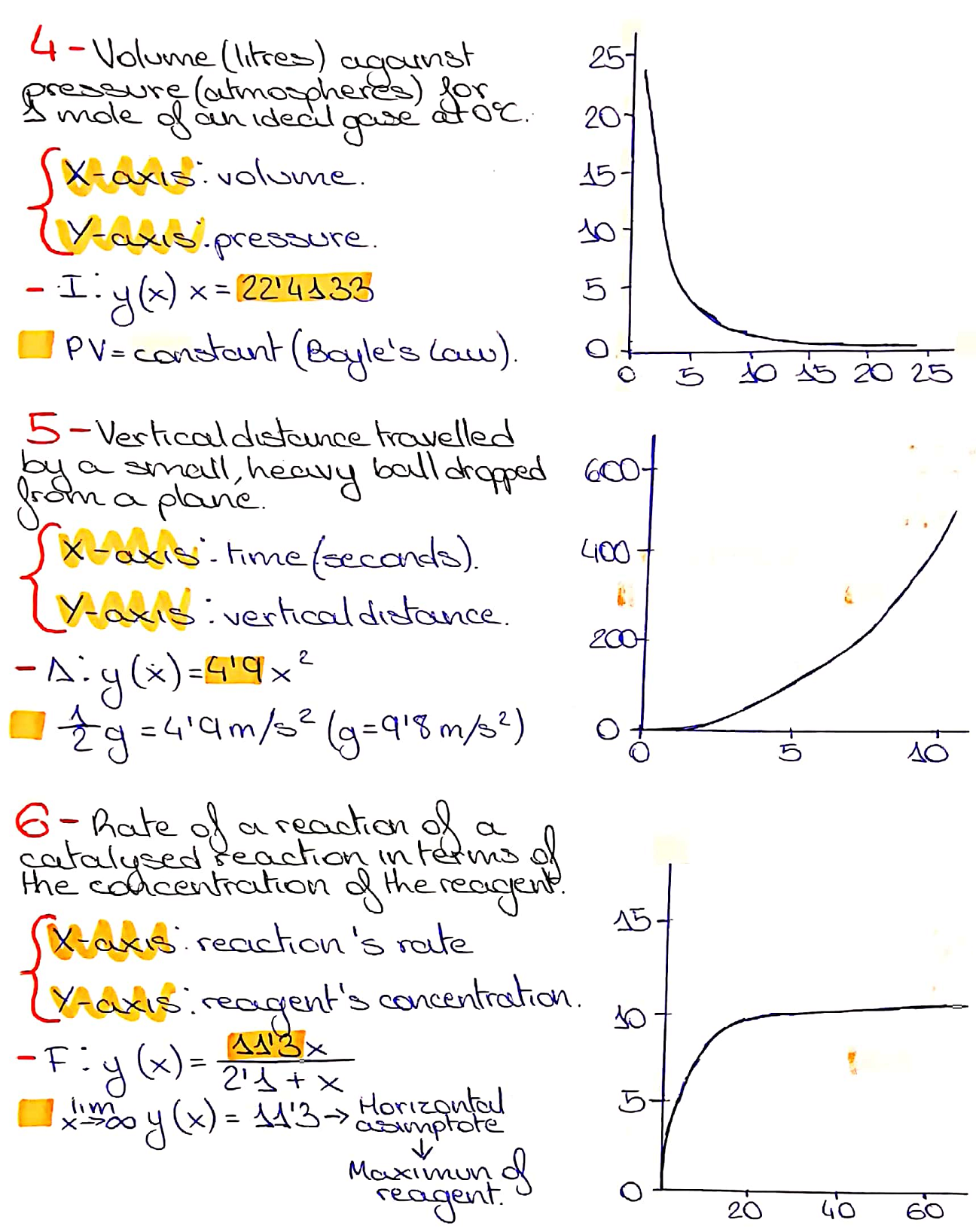
For processes 4, 5 and 6, Raquel correctly identified the correct equations and graphs. Here is Raquel's work (click on the image to open a larger version):
Raquel and Rishik both identified the graph for process 7 correctly. Below is Raquel's work which also includes the equation (click on the image to open a larger version):
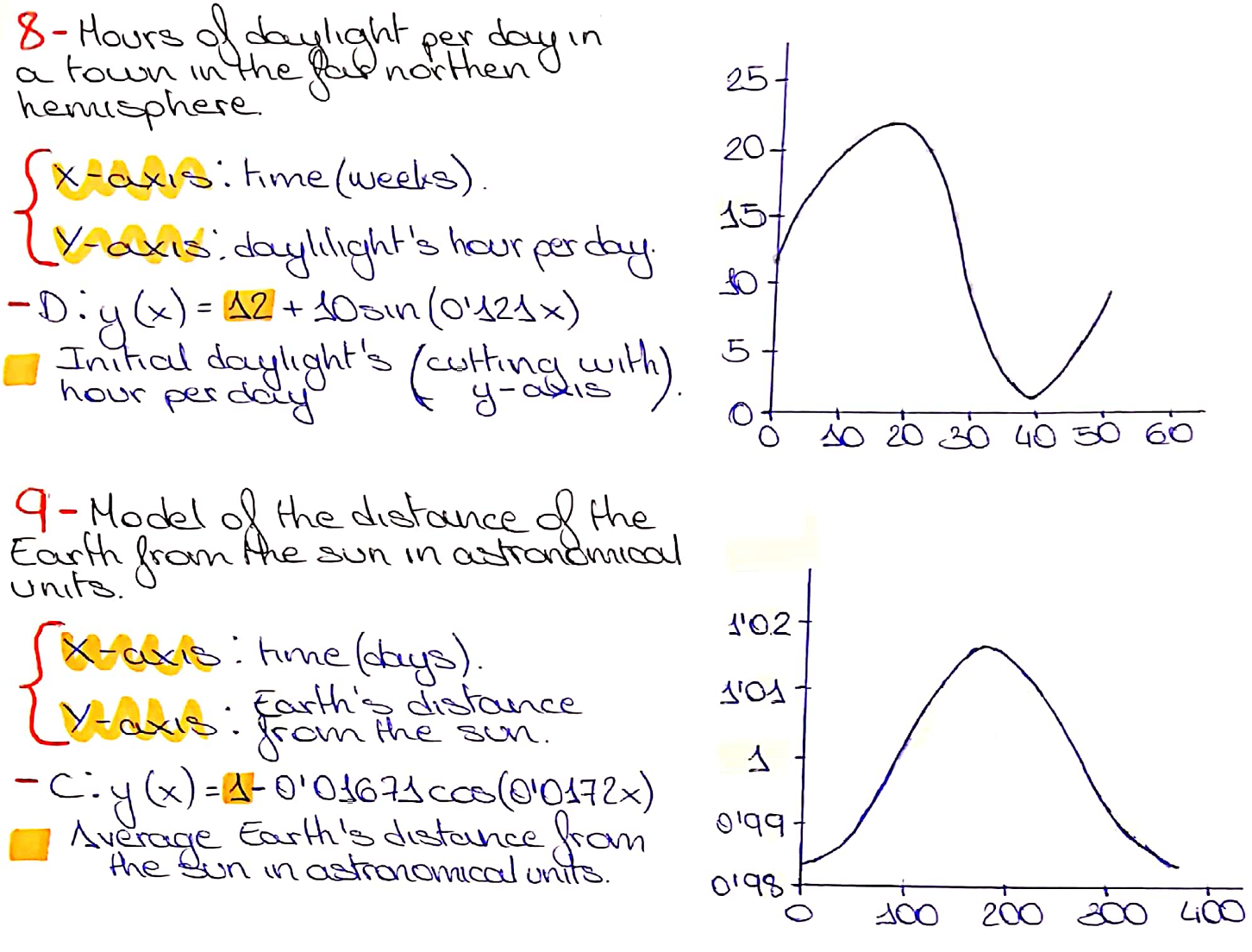
For process 8, Rachel and Rishik agreed about the general shape of the graph, and Rachel chose the graph with the correct units. Here is Rachel's work for processes 8 and 9 (click on the image to open a larger version):