Copyright © University of Cambridge. All rights reserved.
'The Right Volume' printed from https://nrich.maths.org/
Show menu
If we suppose that the curve $y=f(x)$ is integrable then the volume created will be
$$
V = \int^1_0 \pi y^2 dx\;.
$$
To get a feel for the sort of curve we might need, first consider the special case $y=x$, which clearly passes through the two points. Then,
$$
V = \int^1_0 \pi x^2 = \pi\left[\frac{x^3}{3}\right]^1_0 = \frac{\pi}{3}\;.
$$
This is slightly larger than $1$, so we could consider a family of curves which are beneath $y=x$.
We could look for a curve like the blue one in the diagram below:
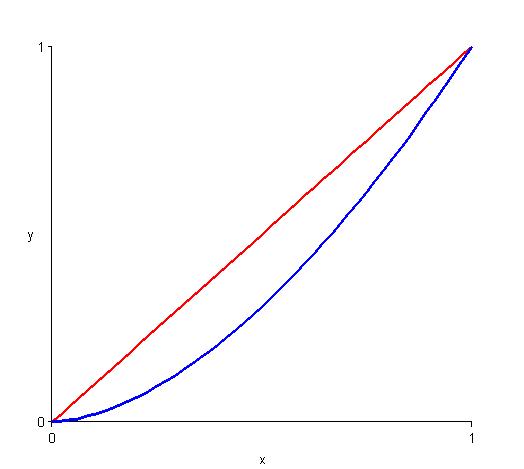
This looks like a section of a polynomial which has a root at $0$.
How about $y=x^4$?
Then,
$$
V = \int^1_0 \pi x^8 = \pi\left[\frac{x^9}{9}\right]^1_0 = \frac{\pi}{9}\;.
$$
This is still not right, but I think a polynomial could work.
Let's try $y=x^a$ where $a$ is a real number.
Then,
$$
V = \int^1_0 \pi x^{2a} = \pi\left[\frac{x^{2a+1}}{2a+1}\right]^1_0 = \frac{\pi}{2a+1}\;.
$$
If we let $a=(\pi-1)/2$ then the volume is $1$.
Therefore a solution is$$
There are, of course, others!
$$
V = \int^1_0 \pi y^2 dx\;.
$$
To get a feel for the sort of curve we might need, first consider the special case $y=x$, which clearly passes through the two points. Then,
$$
V = \int^1_0 \pi x^2 = \pi\left[\frac{x^3}{3}\right]^1_0 = \frac{\pi}{3}\;.
$$
This is slightly larger than $1$, so we could consider a family of curves which are beneath $y=x$.
We could look for a curve like the blue one in the diagram below:

This looks like a section of a polynomial which has a root at $0$.
How about $y=x^4$?
Then,
$$
V = \int^1_0 \pi x^8 = \pi\left[\frac{x^9}{9}\right]^1_0 = \frac{\pi}{9}\;.
$$
This is still not right, but I think a polynomial could work.
Let's try $y=x^a$ where $a$ is a real number.
Then,
$$
V = \int^1_0 \pi x^{2a} = \pi\left[\frac{x^{2a+1}}{2a+1}\right]^1_0 = \frac{\pi}{2a+1}\;.
$$
If we let $a=(\pi-1)/2$ then the volume is $1$.
Therefore a solution is
$$
y=x^{(\pi-1)/2}\;.
$$
There are, of course, others!