Building gnomons
Build gnomons that are related to the Fibonacci sequence and try to
explain why this is possible.
Problem
In this problem, we will use the word "Gnomon" to describe a rectangle which has another rectangle cut out of one of its corners, like this:
Image

I can make gnomons by joining small squares on a grid, so that the areas of my gnomons are all Fibonacci numbers. Fibonacci numbers belong to a sequence where each new number is made by adding together the last two numbers in the sequence - $1,1,2,3,5,8,13...$.
Check that you understand how the sequence works before going any further.
Here is a picture showing the first few gnomons with areas $3,5,8,13$ and $21$
Image

These gnomons are special because each one is made by fitting together the previous two gnomons.For example:
Image
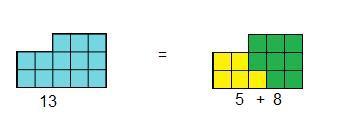
Investigate ways of making each gnomon in the Fibonacci sequence by reflecting and rotating the previous two gnomons to fit them together.
Can you describe how the tenth and eleventh gnomons in my sequence would fit together to make gnomon twelve?
I have noticed that the edges of my gnomons always seem to be Fibonacci numbers. For example, the fifth gnomon in the picture above has two sides with length $2$, two sides with length $3$ and two sides with length $5$.
$2,3$ and $5$ are all Fibonacci numbers. Will this always be the case?
How could you use Fibonacci numbers to work out perimeters of larger gnomons?
Getting Started
Image
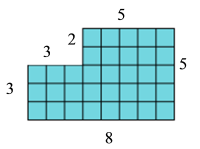
Here are the perimeters of $G_6$.
Image

Here are the perimeters of $G_6$ rewritten in terms of their Fibonacci numbers ($F_1 = 1, F_2 = 1, F_3 = 2, F_4 =3$ and so on).
Can you draw a diagram showing what happens more generally?
Student Solutions
Yana sent in the following ideas about this problem:
In order to make gnomon twelve, the tenth gnomon would have to be reflected and the eleventh gnomon rotated 90 degrees anticlockwise. This is due to a pattern that can be seen after trying to fit together a few of the smaller gnomons.
In the first pair, when you use gnomons with areas 3 and 5 to make a gnomon with area 8, the gnomon with the smaller area is rotated and the one with the larger area is reflected. In the next pair it is the other way round and in the pair of gnomons after that, the smaller one is rotated and the other one reflected again and so on.
You can use Fibonacci numbers to work out perimeters of larger gnomons. First, you can make a table of the lengths (in terms of Fibonacci numbers, i.e. $F_1=1, F_2=1, F_3=2, F_4=3,$ etc.) of the different sides of gnomons, starting from the gnomon with the area of 3, to see if there is a pattern.
1) $2F_1, 2F_2, 2F_3$
2) $F_1, 2F_2, 2F_3, F_4$
3) $2F_2, 2F_3, 2F_4$
4) $F_2, 2F_3, 2F_4, F_5$
5) $2F_3, 2F_4, 2F_5$
6) $F_3, 2F_4, 2F_5, F_6$
7) $2F_4, 2F_5, 2F_6$
Two different patterns emerge. There is one pattern for gnomons with an odd index number and another for gnomons with an even index number. These patterns can be expressed in terms of $F_n$ and $F_m$ on diagrams to show what happens more generally and how the lengths of certain sides change (where $n$ stands for the number of the gnomon in the sequence of those with an odd index number and $m$ is the number of the gnomon in the sequence of those with an even index number).
Image

Excellent thinking, Yana!
Rosie from Edinburgh finished off Yana's thinking.
If we label the blocks as $B_{2n}$ and $B_{2n+1}$. So for the gnomon with area $3$, then $n=0$ and we will label this block $B_1$. With this naming convention, it is the value of $n$ that says how long the sides should be. Now:
Image
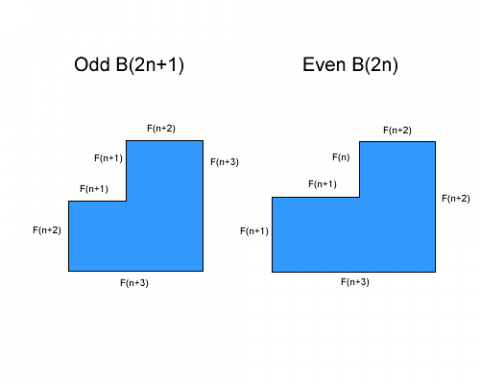
So now we can see really clearly where they will fit together. If we are making an even gnomon, say 12, then we can use as above. $n$ becomes 5, and we can see if the even block is reflected in a vertical axis, and then the odd block rotated $90^\circ$ anitclockwise then they will fit together, as $2n, 2n+1$ are consecutive numbers. To make an odd number block we want $2n-1$ rather than $2n+1$, as we want the consecutive numbers $2n-1, 2n$. Replace $n$ with $n-1$ throughout the diagram, and it will still work. Then as above the smaller block is reflected, and then the larger block is rotated and then they are joined.
From these we can see the edges will always be fibonacci numbers. If you combine the blocks together, you get all edges as a sum of two consecutive fibonacci numbers ($F_{n+3}+F_{n+2}=F_{n+4}$ in the above).
Perimeters:
In the odd example, the perimeter is
$P_O=2\times (F_{n+1}+F_{n+2}+F_{n+3})$
$P_O=4\times F_{n+3}$
as $F_{n+1}+F_{n+2}=F_{n+3}$
In the even example, the perimeter is
$P_E=F_n+F_{n+3}+2\times (F_{n+1}+F_{n+2})$
$P_E=2\times F_{n+4}$
as $(F_n+F_{n+1})+(F_{n+1}+F_{n+2})=F_{n+2}+F_{n+3}=F_{n+4}$
So now all we need to know is how to calculate the $n^{th}$ fibonacci number.
I looked this up on the internet, and its known as Binet's number, and uses the golden ratio Phi.
Phi is
Image
then the formula is
Image
So now we can calculate the perimeters of large gnomons.
Teachers' Resources
Why do this problem?
This problem is about investigating a numerical sequence using pictorial representations. Learners investigate the reflections and rotations needed to combine two consecutive pictures in the sequence to make the next, thus gaining a deeper understanding of the structure of the Fibonacci numbers. Learners may describe patterns in the sequence using their own symbolic representations.Possible approach
Write up the sequence $1, 1, 2, 3, 5$ on the board. Ask for
suggestions as to what might come next, with reasons why. Reveal
that the sequence we are investigating is the Fibonacci sequence
made by adding together the previous two terms of the sequence
(starting with 0,1).
Show the picture of the gnomons and allow the class some time
to experiment until they can find ways of transforming two
consecutive gnomons into the next one. It is important to have some
sense of the orientation of the gnomon - the diagrams in the
problem all have the missing part of the rectangle in the top left,
so this convention could be adopted. The idea is to come up with a
set of instructions which describes how to manipulate
two consecutive gnomons to make the next gnomon in the sequence.
Learners may adopt shorthand ways of writing any reflections and
rotations they have used, but it is important that they are
accurate in their recording in order to spot (and later justify)
patterns. One way of checking the accuracy of their recording is
for everyone to swap their instructions with someone else to see if
they make sense when followed to the letter.
The second part of the problem starts to look at the lengths
of the sides of the gnomons and investigate the Fibonacci sequence.
The key is to come up with a systematic way of recording the edges
in terms of the Fibonacci numbers; there is a diagram in the Hint
which may help.
Key questions
Can you describe how
you have joined your gnomons to make the next one in the sequence
in a way that other people can understand?
Is there more than one way of joining gnomons?
Can you generate all the gnomons using the same process each
time?
Possible extension
Gnomon
Dimensions looks at more patterns and generalisations that can
be made.
