Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
The Pillar of Chios
Age 14 to 16
Challenge Level 





- Problem
- Student Solutions
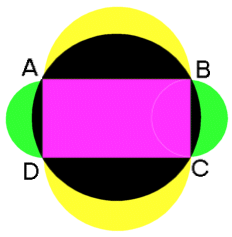
The whole shape is made up of a rectangle, two semicircles on $AB$ and on $DC$ together making one circle, and the two semicircles on $AD$ and $BC$ making another circle.
Excellent solutions were sent in by a pupil from Dr Challoner's Grammar School, Amersham and Nisha Doshi ,Y9, The Mount School, York. Here is one of their solutions: Take: $AB=2x, AD=2y$.
\begin{eqnarray} \mbox{Total area of shape}
&=& \pi x^2 + \pi y^2 + (2x \times\ 2y)\\ &=& \pi
x^2 + \pi y^2 + 4xy. \end{eqnarray}
By Pythagoras Theorem
\begin{eqnarray} AC^2 &=& AD^2 + DC^2\\
&=& (2x)^2 +\ (2y)^2\\ &=& 4(x^2 + y^2)\\
\mbox{Area of big circle} &=& \pi(\mbox{AC}/2)^2\\
&=& \pi(x^2 + y^2)\\ \mbox{Area of crescents} &=&
\mbox{Area of shape - Area of big circle}\\ &=& \pi x^2 +
\pi y^2 + 4xy - \pi (x^2 + y^2)\\ &=& 4xy\\ \mbox{Area of
rectangle} &=& 2x \times\ 2y\\ &=& 4xy
\end{eqnarray}
so the sum of the areas of the four crescents is equal in area to
the rectangle $ABCD$.