Copyright © University of Cambridge. All rights reserved.
'At Right Angles' printed from https://nrich.maths.org/
Show menu
At Right Angles printable sheet
This problem follows on from How Steep is the Slope?
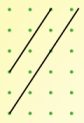
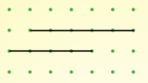
It's easy to draw parallel lines - just check that the gradients match.
 |
 |
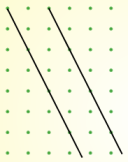 |
| Gradient $\frac{3}{2}$ | Gradient $0$ | Gradient $-2$ |
But I'm finding it harder to draw perpendicular lines. Here are my best efforts so far but I don't think they're quite right!
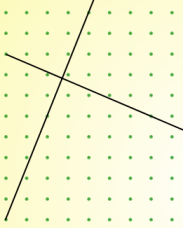
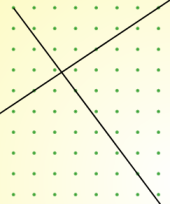
I know that the sides of a square are at right angles, so if I learn to draw tilted squares I may be able to find an efficient method for drawing perpendicular lines.
Experiment with the interactivity below until you can draw squares with confidence.
Work out the gradients of the lines which form your squares.
Is there a relationship between the gradients of perpendicular lines?
Can you use your relationship to explain why the two sets of lines above are not perpendicular?
Full Screen Version
| First line | Second line | ||||||||
| Through (6,9) and (10,1) | Through (4,2) and (14,7) | ||||||||
| Through (6,8) and (21,12) | Through (1,4) and (5,14) | ||||||||
| Through (-3,-2) and (-1,1) | Through (6,1) and (15,-5) |