Thinking Through, and By, Visualising

'Thinking Through, and By, Visualising' printed from https://nrich.maths.org/

Show menu

This article first appeared in Mathematics Teaching 207, published by the Association of Teachers of Mathematics .

We rely on visualising when we solve problems. Sometimes we create an image of the situation that is being discussed in order to make sense of it; sometimes we need to visualise a model that can represent the situation mathematically before we can begin to develop it, and sometimes we visualise to see 'what will happen if ...?'. But are there other ways in which we visualise when solving mathematical problems and if so how can we encourage, value and develop visualising in our classrooms?

This article is based on some of the ideas that emerged during the production of a book (and accompanying CD) which takes visualising as its focus (Piggott and Pumfrey, 2007). It was while we were working on this book we began to identify problems which helped us to take a structured view of the purposes and skills of visualising that we thought worth sharing with you.

Some background

We often associate visualising in mathematics with drawing pictures or diagrams as an aid to getting started on problems. But visualising has a much wider role to play in problem solving including supporting the development of ideas and facilitating communication of results and understanding. In these senses it is not just about pictures and diagrams.

For example, sometimes we place particular emphasis on using visualising to help understand and develop a plan to solve a problem. In producing such a visualisation, the problem solver is identifying the key components of the problem and the relationships between them. This process has two main elements:

an internal model or visualisation (described as imagery by Crapo et al. (2000))
an external representation (described as a visualisation by Crapo et al. (2000)).

Crapo et al. emphasise the importance of the interplay between these internal and external representations which support the development of an effective model. Key to this is both the physical representation which sparks ideas about how the model can be improved, and also discussion and communication with others to come to a shared visualisation.

If we want learners to utilise and improve their capacity to visualise, we need to identify why visualisation is important (the purposes of visualising) and what visualising skills we want our pupils to develop. To do this we need to know what a visualising opportunity is, make that opportunity available and have a language with which to talk about it.

Purposes of visualising

We have been able to identify three purposes for visualising:

to step into a problem,
to model,
to plan ahead.

The first of these purposes relates closely to the idea of 'getting started'. The second and third purposes go beyond this and suggest that visualising occurs in the depth of problem solving, not just at the beginning.

Visualising to step into the problem:

Here visualisations are used to help with understanding what the problem is about. The visualisation gives pupils the space to go deep into the situation to clarify and support their understanding before any generalisation can happen. For example:

One out some under:

Imagine a stack of twenty cards in numerical order (1 at top to 20 at bottom).

Imagine the cards being dealt - one out, one under, one out, one under, one out, one under ...

What would be the last card left in your hand?

Investigate piles of different numbers of cards and justify any rules you discover. In particular:

With a stack of one hundred cards what is the last card left in your hand?
A stack of a thousand cards - what would be the last card left in your hand this time?
Can you always predict which will be the final card in your hand no matter how many there are in the pack?

An introduction to the problem might be:

Imagine a stack of 10 cards in order from 1 (Ace) on the top to 10 on the bottom.

Remove the top card and put it on the bottom.

What is the card on the top now?

Repeat this process, carrying on from where you finished, but this time move four cards.

What is the card on the top this time?

And again, this time move six cards.

What is the number on the top now?

Repeat with different numbers of cards until the class can confidently predict the top card.

The visualisation moves on to a pile of 4 then 8 cards using the rule 'one out - one under'.

The pupils are led through the context with a simple example. The teacher models the process being investigated with frequent pauses to check for understanding. Whilst the teacher is demonstrating, the pupils are asked to visualise and describe what will happen next. The teacher's actions give a focus, and a motivation for the visualisation and enable immediate feedback. The use of language to explain what is seen 'in the mind's eye' also helps with reinforcing the process. Pupils are being encouraged to make sense of the situation through the visualisation.

Visualising to model a situation:

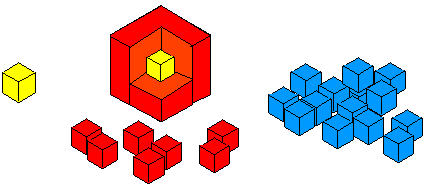
This is particularly useful when the situation is physically unattainable, in other words to try to see the 'unseeable', for example the inside of a 3D object, or considering a case involving a very large number. To illustrate this, have a look at the problem Cubes Within Cubes .

Supporting pupils in modelling situations

Ask the children to imagine they have an unlimited supply of interlocking cubes (all the same size) in different colours.

Invite them to imagine starting with one yellow cube.

This is covered all over with a single layer of red cubes.

Describe what you see:

How many red cubes touch the yellow cube face-to face?
How do the cubes along the edge of the red cube touch the yellow cube?
How many red cubes touch the yellow cube in this way (careful)?
How do the red cubes in the corners of the large red cube touch the yellow cube?
How many touch in this way?
How many red cubes are there altogether?
How many red and yellow cubes?
Can you explain why?

In this example it is not possible to 'see inside' a large cube and, although smaller cubes can be constructed as the layers increase, it is not possible to see the centre cube at the same time as the surrounding layer. The modelling in this problem is two-fold. Initially the pupils are encouraged to think in stages and later to use the visualising strategies to tackle the main problem. An outcome of the lesson can be pupil production of story boards as representations of the visualisations and stages they used whilst problem solving. These images have two aspects:

they reflect the imagery the pupils used,
they represent the route the pupils may have taken to obtain their solution.

In this particular problem, there are multiple representations and there are potentially multiple routes to a solution. For example in the figure below, pupils show two different ways of describing the number of surrounding cubes:

Visualising to plan ahead:

This involves using visualising during the problem-solving process to anticipate. In other words asking yourself: 'What will be the consequence if I do this?'. This is related to problem posing 'What would happen if ...?'. It is not possible to ask the question 'What if?', if you have not thought ahead and any thinking ahead necessarily includes visualisation. For example, have a go at the problem Frogs .

Supporting pupils in thinking ahead:

What would be your first move?
Your second move?
Is there more than one option for the next move?
What if I move the frog to here next?
Does it matter which move you choose when you do have a choice? ...

To answer a question like 'What if I move the frog to here next?', I would need to be aware that this is one of several possibilities and therefore have a visualisation of the wider context of the problem (as opposed to a form of tunnel vision - going for the first thing that comes into your head). A lesson plenary could focus on a solution to the problem, but there is also the opportunity to discuss the range of recording systems the pupils adopt and the role of thinking ahead.

Visualising skills

We have spoken about why you might visualise. But, what are the underpinning skills that support the visualising when problem solving? That is, the ways in which we visualise as we step into, model and plan. We have started to think about specific visualising skills that we should be offering opportunities for our pupils to practise and hone.

Internalising: Like the 'imagery' of Crapo et al (2000) this involves being able to (close your eyes) and focus on a problem, then pick out salient features to represent and make sense of the situation. In the problem Cubes Within Cubes it is necessary to spend the time creating an internal representation that you can draw on as you work through the problem. Without this internal image any ownership of the generalisation seems impossible.

Identifying : Being able to identify a useful image or representation of an idea, which may be someone else's, that means something to you. This representation helps you see or describe the structure of a problem. This is why a teacher might produce diagrams and images to support their pupils - sharing their visualisation may help learners to access the problem situation.

Comparing : Being able to scrutinise different images to identify what is the same or different, including:

Being able to compare other people's representations with our own. For example in Cubes Within Cubes , comparing the two visualisations given above with your own.
Being able to identify the general and the specific in a representation and their significance in terms of the problem at hand. For example in a problem involving polyominoes, you might start with a domino (from which you are going to build triominoes), asking learners to visualise putting two squares together. Recognition that there is an infinite number of orientations (general) is important but, in preparing to build triominoes, you only need to consider one orientation and to have that very clearly in your mind.
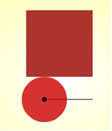
Trying to hold more than one image in your head. For example: remembering a starting point and being able to 'rewind' when a sequence of moves does not work; keeping more than one aspect of the problem in 'view'. For example in the problem Roundabout the visualisation requires you to be thinking about both the circle moving round and the locus its centre makes.

Connecting : Being able to make connections by remembering the processes or underpinning structure rather than individual images. For example, it is possible to build all the hexominoes given all the pentominoes. The underpinning structure involves the visualisation of each pentomino (which could involve the visualisation of each tetromino ...). On top of the pentomino structure is superimposed a system for systematically generating all the hexominoes. In this case it might be by visualising the movement of a sixth square around each pentomino to produce a family of 'related' hexominoes.

Sharing : Being able to describe a personal visualisation to an audience. This may be necessary when trying to explain or clarify thinking or share an interpretation. There are times when the visualisation is not simply an image but has an element of variation. For example in the problem Roundabout the visualisation might include the effect of enlarging or shrinking the square (or circle).

The skills underpin the processes, which extend beyond using images and diagrams to help familiarise the problem solver with the problem situation. Visualising is at the heart of problem solving itself.

There is more to visualising than meets the eye!