 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Tied Up



- Problem
- Solutions
Neither of the sheep can reach all of the points in the field:
Showing why using circles
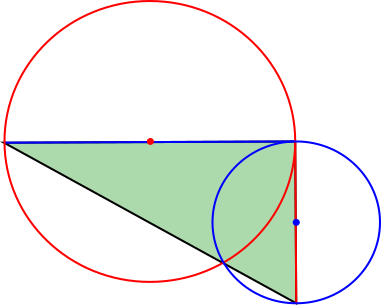 The red and blue circles show the boundaries of the areas the sheep can reach.
The red and blue circles show the boundaries of the areas the sheep can reach.
Because the triangle is right-angled, the red side is a tangent to the red circle. So the sheep in the red circle can't reach any other points on the red side, because the tangent only touches the circle once.
Similarly the blue side is a tangent to the blue circle, so the sheep in the blue circle can't reach any other points on the blue side.
Showing why using triangles
If either sheep can reach all of the points in the field, then that sheep would be able to reach the vertex opposite the place it is tied.
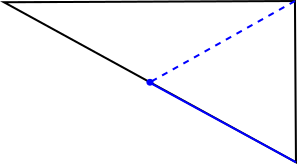
In the diagrams below, the solid lines represent the lengths of the ropes, and the dotted lines represent the distance to the opposite vertex.


The blue and red triangles shaded are both right-angled triangles, since they both contain the right angle from the original triangle. But the dotted lines are the hypotenuses - so they must be longer than the ropes. So neither sheep can reach all of the points in the field.
Explanation using circle theorems
A circle centred at the midpoint of the hypotenuse marks the boundary of the area the goat can reach.
Will the vertex at the right angle be inside, outside or on this circle?



The hypotenuse of the triangle is the diameter of the circle, so the right angle is at the circumference.
This shows that the goat can just reach the far vertex, and therefore the whold field fits within reach of the goat's rope.
Explanation using triangles, which also proves the circle theorem used above
 On the right, the goat's rope is shown as a solid blue line and the distance from the goat's post to the far vertex is shown as a dotted blue line.
On the right, the goat's rope is shown as a solid blue line and the distance from the goat's post to the far vertex is shown as a dotted blue line.Drawing some horizontal and verical lines (parallel to the triangles sides), we can split the triangle into four smaller triangles, each similar to the whole triangle, as shown:
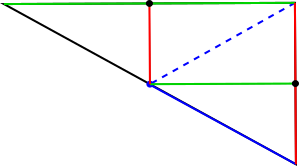
The red line segments are all of equal length, and so are the green ones, so since the four little triangles all have right angles, they are all congruent.
This means the dotted line is the same length as the goat's rope.
The hypotenuse of each little triangle is the longest line within the triangle, so since the goat's rope is as long as this hypotenuse, the goat can reach all the points in the field.