Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Immersion
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
To begin, we can work out the volume of each solid:
Solid 1) A sphere of radius $1 \ \mathrm{cm}$ :
$$\textrm{[Volume]} = \frac{4}{3}\pi r^3 = \frac{4}{3}\pi \ \mathrm{cm^3}$$
Solid 2) A solid cylinder of height $\frac{4}{3} \ \mathrm{cm}$ and radius $1 \ \mathrm{cm}$:
$$\textrm{[Volume]} = \pi r^2 h = \frac{4}{3}\pi \ \mathrm{cm^3}$$
Solid 3) A solid circular cone of base radius $1 \ \mathrm{cm}$ and height $4 \ \mathrm{cm}$.
$$\textrm{[Volume]} = \frac{1}{3} \times \textrm{[Volume of a cylinder]} = \frac{1}{3}\pi r^2 h = \frac{4}{3}\pi \ \mathrm{cm^3}$$
Solid 4) A solid cylinder of height $\frac{4}{9}\ \mathrm{cm}$ with a hole drilled through it, leaving an annular cross-section with interal and external radii $2 \ \mathrm{cm}$ and $1 \ \mathrm{cm}$.
$$
\begin{align}
\textrm{[Volume]} & = \textrm{[Volume of the outer cylinder]} - \textrm{[Volume of the inner cylinder]} \\
& = \pi (r_{outer}^{2} - r_{inner}^{2}) h = \frac{4}{3}\pi \mathrm{\ cm^3}\\
\end{align}
$$
We can now work out what the axes represent:
$y$-axis:
The maximum $y$ value reached by all curves is identical at around 4.2, it is in fact equal to $\frac{4}{3}\pi$. This suggests the y axis is a measure of volume, all solids will eventually displace a fluid of $\frac{4}{3}\pi \mathrm{\ cm^3}$.
The $y$ axis represents the volume of fluid displaced (or the volume of the solid immersed) in $\mathrm{cm^3}$.
$x$-axis:
The $x$-axis represents the time elapsed in minutes since lowering began.
Simon now works out which curve matches which solid, with some clear reasoning:
Curve 1:
The time taken to fully immerse the object $\approx 1.3 \mathrm{\ minutes}$
The volume displaced varies linearly with time, this must therefore represent:
Solid 2 (cylinder of height $\frac{4}{3} \mathrm{\ cm}$ and radius $1 \mathrm{\ cm}$) lowered vertically
or
Solid 4 (A solid cylinder of height $\frac{4}{9} \mathrm{\ cm}$ with a hole drilled through it) lowered vertically.
The time taken to fully immerse the object = $\frac{4}{3}\pi \mathrm{\ minutes}$
Curve 1 is therefore a cylinder of height $\frac{4}{3} \mathrm{\ cm}$ and radius $1 \mathrm{\ cm}$ lowered vertically
Curve 2 and Curve 3:
The time taken to fully immerse the object = $2 \mathrm{\ minutes}$
This could therefore be:
Solid 2 lowered sideways or solid 1 lowered in any orientation.
Solid 2 lowered sideways would initially displace a greater fluid than solid 1, it can therefore be seen that curve 2 corresponds to solid 2 lowered sideways and curve 3 to solid 1.
Curve 4 and Curve 5:
The time taken to fully immerse the object = $4 \mathrm{\ minutes}$
This could therefore be:
Solid 3 lowered vertically or solid 4 lowered sideways
Consider solid 3 lowered vertically:
Volume immersed as a function of height ($h$)
$$V(h) = \frac{1}{3}\pi r^2 h$$
If we immerse this cone point first the radius varies with the height of object immersed as:
$$r = \frac{h}{4}$$
$$V(h) = \frac{\pi h^3}{48} \textrm{ or } V(t) = \frac{\pi t^3}{48} \ (\textrm{as } 1 = \frac{h}{t})$$
Solid 3 immersed point first must therefore be curve 5 which leaves solid 4 lowered vertically as curve 4.
It is possible to find algebraic forms for the volume displaced at height h as shown below, although this is very involved for some of the solids!
Curve 1:
Cylinder of height $\frac{4}{3} \mathrm{\ cm}$ and radius $1 \mathrm{\ cm}$ lowered vertically.
$$V(h) = \pi h$$
Curve 2:
A solid cylinder of height $\frac{4}{3} \mathrm{\ cm}$ and radius $1 \mathrm{\ cm}$ lowered sideways
The volume immersed equals the length of cylinder multiplied by the area of a segment
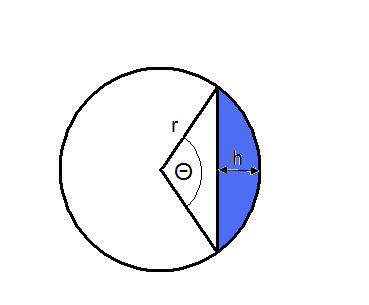
From the geometry it can be seen that $\cos(\frac{\theta}{2}) = (1-h)$
$\theta = 2\arccos(1-h)$
$\textrm{[Area of segment]} = 0.5(r^2\theta -r^2 \sin(\theta)) = 0.5(2\arccos(1-h) - \sin(2\arccos(1-h))$
$\sin\theta = 2 \sin\frac{\theta}{2} \cos\frac{\theta}{2}$
$\sin\frac{\theta}{2} = \sqrt{1 - \cos^2\frac{\theta}{2}}$
$\sin(2 \arccos(1-h)) = 2\sqrt{1 - (1-h)^2} (1-h) $
$\textrm{[Area of segment]} = 0.5(r^2\theta -r^2 \sin(\theta)) = 0.5(2\arccos(1-h) - \sin(2\arccos(1-h))$
$\textrm{[Area of segment]} = \frac{1}{2}( 2\arccos(1-h) - 2\sqrt{1 - (1-h)^2}) (1-h)$
The volume immersed equals the length of the cylinder multiplied by the area of the segment
$\textrm{[Volume at h]} = \frac{2}{3}( 2\arccos(1-h) - 2\sqrt{1 - (1-h)^2}) (1-h)$
Curve 3:
A sphere of radius $1 \mathrm{\ cm}$
The volume immersed as a function of h is equal to the volume generated when we rotate the equation of a circle about the $x$-axis by 360 degrees and evaluate this integral between the limits $r$ and $(r-h)$.
Equation of circle: $y^2 + x^2 = r^2 = 1$
$$\textrm{[Volume]} = \int_{1-h}^{1} \pi f(x)^2 \ \mathrm{d}x = \int_{1-h}^{1} \pi (1-x^2) \ \mathrm{d}x =\pi \left[ x - \frac{x^3}{3} \right]^{1} _{1-h} = \pi h^2(1-\frac{h}{3})$$
Curve 4:
A solid cylinder of height $\frac{4}{9} \mathrm{\ cm}$ with a hole drilled through it, leaving an annular cross-section with interal and external radii $2 \mathrm{\ cm}$ and $1 \mathrm{\ cm}$ lowered sideways.
When $h$ is less than $1 \mathrm{\ cm}$ the volume immersed takes the same form as curve 2 but simply changing the radius from $1 \mathrm{\ cm}$ to $2 \mathrm{\ cm}$ and changing the length of the solid from $\frac{4}{3} \mathrm{\ cm}$ to $\frac{4}{9} \mathrm{\ cm}$.

From the geometry we see that:
$\cos(\frac{\theta}{2}) = \frac{2 - h}{2}$
$\theta = 2 \arccos(1-0.5h)$
$A(h) = 0.5(r^2\theta -r^2 \sin\theta) = 0.5(8 \arccos(1- 0.5h) - 4 \sin (2 \arccos(1-0.5h))$
$\sin\theta = 2\sin\frac{\theta}{2} \cos\frac{\theta}{2}$
$\sin\frac{\theta}{2} = \sqrt{1 - \cos^2\frac{\theta}{2}}$
$\sin\theta = 2\sqrt{1 - (1-0.5h)^2} (1-0.5h) $
$\therefore \ A(h) = 4 \arccos(1- 0.5h) - 4(1-0.5h)\sqrt{1 - (1-0.5h)^2}$
$\textrm{[Volume]} = \frac{4}{9} \textrm{[area]} = \frac{16}{9}(\arccos(1- 0.5h) - (1-0.5h)\sqrt{1 - (1-0.5h)^2}$
(when $h$ is less than 1)
When h is greater than $1\mathrm{\ cm}$ the volume immersed can be found by subtracting the area of the inner segment from the outer segment and then multiplying by the length of the cylinder.
Volume of the outer segment is as above:
$\textrm{[Volume]} = \frac{4}{9} \textrm{[area]} = \frac{16}{9}(\arccos(1- 0.5h) - (1-0.5h)\sqrt{1 - (1-0.5h)^2} )$
Volume of inner segment:
From the geometry it can be seen that:
$\theta = 2\arccos(2-h)$
$\textrm{[Volume]} = \frac{4}{9} (0.5(r^2\theta -r^2 \sin\theta)) = \frac{2}{9} ( 2\arccos(2-h) - \sqrt{1 -(2-h)^2})$
Therefore:
$
\begin{align}
\textrm{[Volume immersed]} & = \frac{4}{9}(4\arccos(1- 0.5h) - 4(1-0.5h)\sqrt{1 - (1-0.5h)^2)} \\
& -\arccos(2-h) + 0.5 \sqrt{1 -(2-h)^2} )\\
\end{align}
$
(when $h$ is greater than 1)
Therefore
(when $h$ is less than 1)
$V(h) = \frac{4}{9} \textrm{[area]} = \frac{16}{9}(\arccos(1- 0.5h) - (1-0.5h)\sqrt{1 - (1-0.5h)^2} )$
(when $h$ is greater than 1)
$V(h) = \frac{4}{9}(4\arccos(1- 0.5h) - 4(1-0.5h)\sqrt{1 - (1-0.5h)^2)} -\arccos(2-h) + 0.5 \sqrt{1 -(2-h)^2} )$
Curve 5:
A solid circular cone of base radius $1 \mathrm{\ cm}$ and height $4 \mathrm{\ cm}$ lowered point first.
$V(h) = \frac{1}{3}\pi r^2 h$
$r(h) = \frac{h}{4}$
$V(h) = \frac{\pi h^3}{48} $