A random variable $X$ has a zero probability of taking negative values but has a non-zero probability of taking values in the range $[0, a]$ for every $a>0$. The curve describing the probability density function forms an arc of a circle. Which of these are possible shapes (ignoring the scale) for the probability density function $f(x)$? Identify clearly the mathematical reasons, using the correct terminology, for your answers.


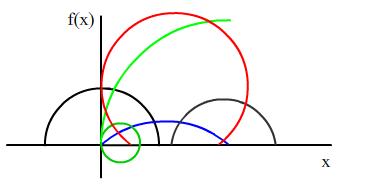
If the radius of the circle forming the arc of the pdf is $1$, what is the maximum value that the random variable could possibly take?

Which of the other arcs are possible candidates for probability density functions? Can you invent mathematical scenarios which would lead to these pdfs?