 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Bessel's Equation



- Problem
Consider the following differential equation (called a Bessel equation)
$$t\frac{d^2 y}{dt^2}+\frac{dy}{dt}+ty=0$$
It is impossible to solve this equation in terms of simple functions, but it is possible to find a solution as a power series. Why not try to solve it to get a feel for the problems involved? Could you explain clearly to someone why the equation is hard to solve?
Although we can't solve it in terms of simple functions, we could look at the equation for very large or very small values of $t$ to try to get an approximate solution at those times. Think about these suggestions:
1. EITHER $y(t)$ or its derivatives are very large for large time $t$
OR $y$ approximately satisfies a simple harmonic motion equation for very large time $t$.
2. EITHER $y$ or its derivatives are very large for very small time $t$
OR $y$ is approximately constant for very small time $t$.
Can you see why these possibilities might make sense?
A power series analysis shows that one of the solutions to the Bessel equation is
$$y_0(t) = 1-\frac{1}{(1!)^2}\left(\frac{t}{2}\right)^2+\frac{1}{(2!)^2}\left(\frac{t}{2}\right)^4-\frac{1}{(3!)^2}\left(\frac{t}{2}\right)^6+\frac{1}{(4!)^2}\left(\frac{t}{2}\right)^8 + \ldots$$
[Note: $n!$, called '$n$-factorial', means $n\times(n-1)\times(n-2)\times \dots \times 2\times 1$]
By working out $t\frac{d^2 y_0}{dt^2}$, $\frac{dy_0}{dt}$ and $ ty_0$ separately, show that the terms of like powers for the first few powers of $t$ all cancel out exactly if we substitute this value for $y_0(t)$ into the Bessel equation.
If this series were to continue in a regular fashion (which it does), what would the next term in the expansion be?
Can you easily determine for sure the behaviour of the function at very small times from the power series?
Can you easily determine for sure the behaviour of the function at very large times from the power series?
The first $150$ terms of the series were plotted on a spreadsheet, resulting in the following two charts: the first is plotted on the range $0\leq x \leq 40$ and the second on the range $0\leq x \leq 45$
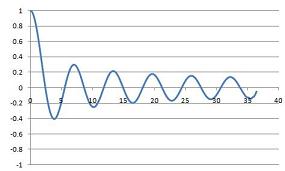 |
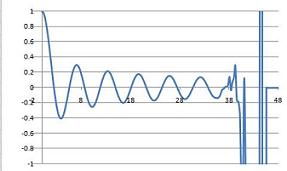 |
What has gone wrong?
NOTES AND BACKGROUND
Bessel was a 19th century astronomer and the first person accurately to predict the distance to a star: using the method of parallax he calculated the 61 Cygni was a mere 9.8 light years away. In engineering and physics, Bessel's equation is of similar importance to the equation for simple harmonic motion; the solutions to Bessel's equation, called Bessel functions, may be though of as time-decaying versions of sine and cosine. They are both theoretically interesting and practically useful.