 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
A Chordingly



- Problem
- Student Solutions
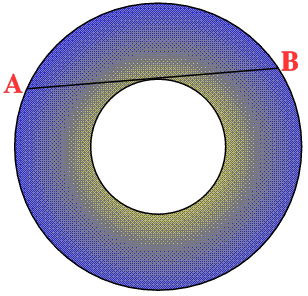
Jessica Zhang of Woodbridge High School, Arwa Jamil , Year 8, the International School Brunei and Nisha Doshi and Suzanne Abbott from Year 9 the Mount School, York all sent good solutions to this problem.
Let the radius of the big circle be $R$ and the radius of the small circle be $r$. By Pythagoras theorem: $$ R^2 - r^2 = ({1\over 2}AB)^2 $$ The area of the big circle is $\pi R^2$ and the area of the small circle is $ \pi r^2 $. The area of the annulus $A$ is the area of the big circle minus the area of the small circle so: $$ A = \pi R^2 - \pi r^2 = \pi (R^2 - r^2) = \pi({1\over 2}AB)^2 = \pi (AB)^2/4. $$
You may also like
The Old Goats
A rectangular field has two posts with a ring on top of each post. There are two quarrelsome goats and plenty of ropes which you can tie to their collars. How can you secure them so they can't fight each other but can reach every corner of the field?
Isosceles
Prove that a triangle with sides of length 5, 5 and 6 has the same area as a triangle with sides of length 5, 5 and 8. Find other pairs of non-congruent isosceles triangles which have equal areas.