Congratulations to Nisha Doshi, Year 9, The Mount School, York for this beautifully explained solution.

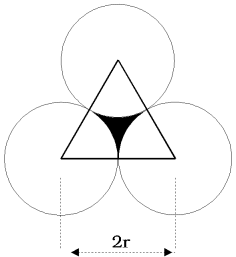
If these triangles are made into a tessellation, they will form regular hexagons with circles overlaid. Each triangle consists of 3 x 1/6 = 1/2 of a circle, plus the shaded area, so to find the area of the shaded section, you can do : (area of triangle - area of 1/2 of a circle)

Using Pythagoras' Theorem the height of the triangle is $\sqrt((2r)^2 - r^2 ) = r\sqrt3$. So the area of the triangle is $r^2\sqrt3$. The area of ${1\over 2}$ a circle is ${1\over 2}\pi r^2$. So the area shaded is $r^2\sqrt3 - {1\over 2}\pi r^2$ and the proportion of the tessellation that is shaded is $$ \frac{r^2\sqrt3 - {1\over 2}\pi r^2}{r^2\sqrt3} = 1 - \frac{\pi}{2\sqrt3} $$

Well done Arwa Jamil, Year 8, the International School Brunei who calculated correctly, to 3 significant figures, that 9.31% of the floor is shaded.