Copyright © University of Cambridge. All rights reserved.
'Searching for Mean(ing)' printed from https://nrich.maths.org/
Show menu
Khue from British Vietnamese International School in Vietnam said:
An easier way of finding a mean weight for a combination of weights that is [the] numbers weights add up to a multiple of 5.
These diagrams illustrate Khue's reasoning:
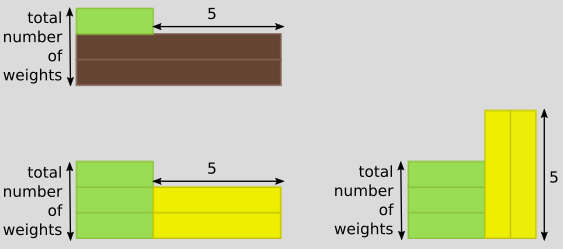
or 
In fact, there are combinations of 3 kg and 8 kg weights which have means equal to 3, 4, 5, 6, 7 and 8 kg. Click to see them all.
Mahdi from Mahatma Gandhi International School in India used algebra to extend the problem to other pairs of weights: