 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Searching for Mean(ing)



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
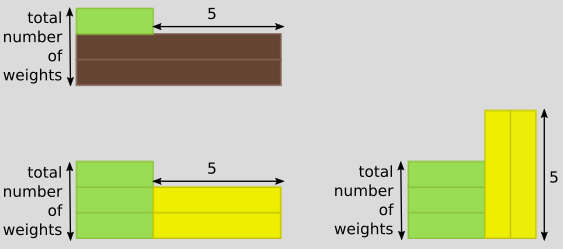
Khue from British Vietnamese International School in Vietnam said:
An easier way of finding a mean weight for a combination of weights that is [the] numbers weights add up to a multiple of 5.
These diagrams illustrate Khue's reasoning:
or 
In fact, there are combinations of 3 kg and 8 kg weights which have means equal to 3, 4, 5, 6, 7 and 8 kg. Click to see them all.
Mahdi from Mahatma Gandhi International School in India used algebra to extend the problem to other pairs of weights:
You may also like

Bat Wings
Two students collected some data on the wingspan of bats, but each lost a measurement. Can you find the missing information?

Kate's Date
When Kate ate a giant date, the average weight of the dates decreased. What was the weight of the date that Kate ate?