 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Searching for Mean(ing)



Searching for Mean(ing) printable sheet
If you have not used the Cuisenaire Environment before, you might find it helpful to look at the instructions and video before trying this problem.
Imagine you have a large supply of 3kg and 8kg weights.
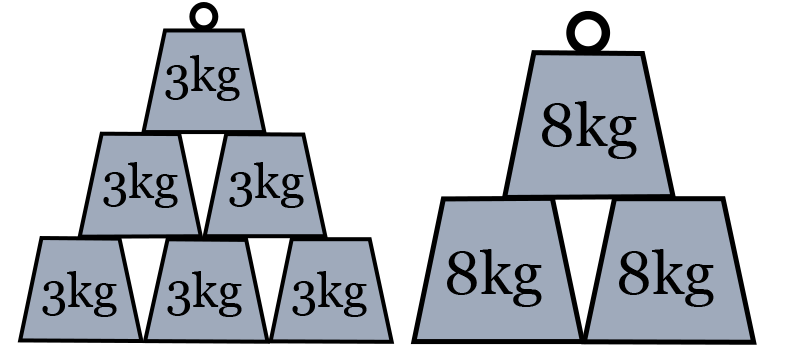
Can you see how the picture below can be used to explain why two 3kg weights and three 8kg weights have a mean weight of 6kg?

Can you find other combinations of 3kg and 8kg weights whose mean weight is a whole number of kg?
What's the smallest possible mean?
What's the largest?
Can you make all the whole numbers in between?
You may wish to use the interactive Cuisenaire environment below.
Now explore some different pairs of weights (for example 2kg and 7kg).
Which whole numbers is it possible to have as the mean weight?
What do you notice about your results?
Can you use what you notice to find the combination of 17kg and 57kg weights that have a mean weight of 44kg......of 52kg.......of 21kg.....?
Explain an efficient way of doing this.
Can you explain why your method works?
Click here for a poster of this problem.