A square of side length 1 has an arc of radius 1 drawn from each of its corners, as in the following diagram. The arcs intersect inside the square at four points, to create the shaded region.

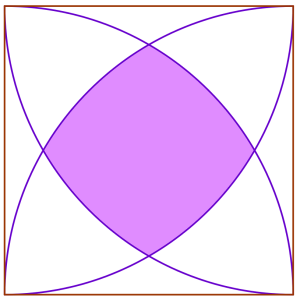
What is the area of the largest square that can be completely contained within the shaded region?

Is this a good estimate of the actual shaded area?

What is the exact area of the central shaded region?
How did that compare to your estimate?

Can you find more than one method to work out the exact area?




Click here for a poster of this problem.