Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Partly Circles
Age 14 to 16
Challenge Level 





Partly Circles printable sheet
Here are three problems involving circles.
Can you solve them?
Can you find relationships between the three problems?
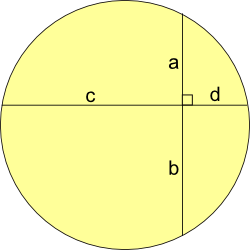
Firstly Show that ab = cd (where a, b, c, d are lengths)
Secondly:
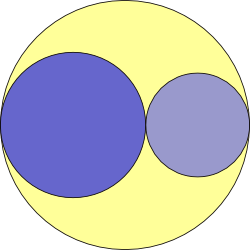
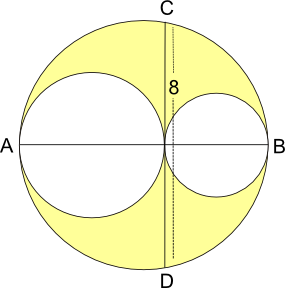
These three circles are drawn so that they touch each other, and their centres are all on the line AB.
If CD is $8$ units in length, what is the area of the region shaded yellow?
Lastly: If the area shaded yellow is equal to the area of the larger of the two blue circles, what is the relationship between the radii of the three circles?