The Four Colour Theorem

Pedagogical Notes

The Four Colour Problem

The possibility that any map could be coloured so that adjacent areas, however they are combined, needs only four colours, is very simple to describe. However, we have seen how extremely difficult it was to prove. In the accompanying article, I have highlighted the essential stages needed before in any proof can be successful, be it in high-level mathematics, or in the classroom. It is also essential to realize that a proof may not last forever. As happened here, different areas of mathematics may influence the way we look at a problem, and precise definition of the things we are dealing with is often quite difficult.

The following notes offer some suggestions for the classroom, and indicate that some of the most apparently abstract ideas can lead to important practical applications.

1. Euler, polyhedra and networks.

Euler's Formula for polyhedra appears in may school textbooks, but often merely as an exercise in filling in a table for the five regular solids. But what, exactly, is a polyhedron? There is plenty of opportunity to show different objects (packaging of various kinds, objects with curved surfaces, cones, pyramids joined at the apex, etc.) to see if they fit the formula, and if they do not, whether we want to call them 'polyhedra', (or even change the conditions for the formula).

Euler is also well-known for the 'Bridges of Konigsberg' problem, but few take the opportunity of linking this with Hamiltonian paths , the Icosian Game and Graph Theory. See http://en.wikipedia.org/wiki/Seven_Bridges_of_Konigsberg .

2.Augustin Cauchy and the transformation of the problem.

Cauchy's original conception which led to his proof of the polyhedron formula was to imagine cutting out a face of the polyhedron and squashing it flat onto the plane, thus obtaining the formula $f + v - e = 1$ (see the example with the cube). It is relatively easy to obtain a picture of a tetrahedron in this way, if you look down on it from above. However, making the maps of other objects is more difficult.

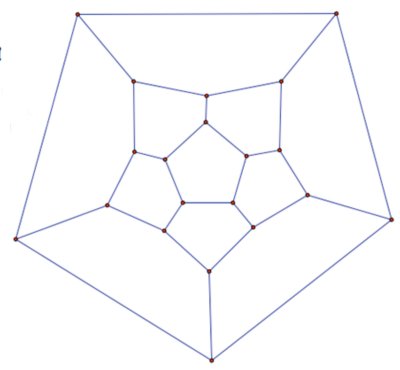A stereographic projection is obtained by projecting all the points on the surface of an object from its 'north pole' onto a plane tangent to its 'south pole'. In this projection of a dodecahedron all the faces remain pentagons.

A projection like this forms a map . It is not the same as the net of the dodecahedron.

Cauchy's proof started by triangulating the faces of the 'squashed' polyhedron and then removing the edges one by one, thus preserving the formula $f + v - e = 1$. However, there are problems. If you triangulate the dodecahedron, and begin to remove the edges, what problems do you encounter, and what can you do about them? Try this with any map (not necessarily representing a polyhedron) does it work?

3. Maps on 'Islands in the sea'

It is relatively easy to find the conditions for two-colouring and three-colouring. Here is a simple 'straight line' map. How many colours are needed here? What about the surrounding 'sea'? Do we include it or not?

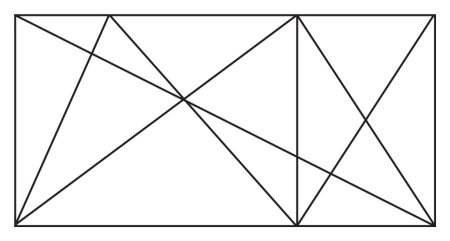Pupils can experiment with other straight line maps. What conditions are required so that only two colours need be used? Try maps with intersecting circles and see if there are any differences.

Try other maps - for example imagine the spokes on a wheel. Can you colour the spaces between the spokes with two colours, or will you need three? The examples given of Cayley's discoveries could help here.

Lewis Carroll's map colouring challenge.

Pupils could use these ideas not just for challenging each other, but also to give the conditions why or why not a map is colourable.

Map colouring in three dimensions

Four-colouring does not work in three dimensions. Frederic Guthrie showed that if the 'countries' were flexible coloured rods, they could be laid to touch each other as often as we like, so that many more colours would be needed. You could think of the 'warp and weft' in weaving or in basket making, where the same strands will touch each other in many places.

However, maps drawn on surfaces which are not topologically equivalent to a sphere, pose more difficult problems. For example, it has been shown that at least seven colours are needed for a map drawn on a torus.

4. Hamiltonian paths and Graph Theory

A Hamiltonian path (circuit or cycle) is a path that visits each vertex of the graph once and only once (except for the vertex which is the start and finish). The path does not have to travel along every edge to complete the circuit.

Note that the graphs shown in the puzzle on the NRICH link are all 'cubic' graphs (each vertex is a meeting point for three edges). Are there any Hamiltonian paths on graphs that are not cubic?

In the 1850s Thomas Kirkman (1805-1895) first studied circuits on polyhedra, and Hamilton produced "The Icosian Game" in 1857 (see Robin Wilson's Four Colours Suffice pages 108-112).

In the 1930s mathematicians began to apply the study of circuits on graphs to the 'Travelling Salesman Problem' to find the most efficient routes for delivering goods to a number of different places.

Since then, Graph Theory has become a large area of mathematics with important applications for example in traffic networks, and information flow, biology, atomic structure, and the design of websites.

Hunting Snarks

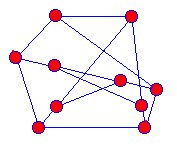This Snark is equivalent to the one in the article. The positions of the vertices may be different, but the connections remain the same. Both graphs have 10 nodes and 15 edges.

You can find out more about snarks, and more examples of them at: http://en.wikipedia.org/wiki/Snark_(graph_theory)

5. Duals and Duality

The idea of a dual in geometry first appeared in the work of Pascal (1623-1662) and Desargues (1591-1661) in the seventeenth century. A good example of the idea in plane geometry is where the pairs of opposite sides of a hexagon can be extended to meet in three points which lie on the same straight line. Pascal Called this the Mysterious Hexagram Theorem. An interactive version of the dual of Pascal's Theorem by Brianchon (1783-1864) can be found at: http://www.cut-the-knot.org/Curriculum/Geometry/Brianchon.shtml

Duals of simple polyhedra are not difficult to visualise. By putting a point in each of the faces of a tetrahedron, and joining the points with lines, we get its dual. For a cube, its dual is an octahedron.

For polyhedra, vertices are exchanged with faces and faces with vertices. By analogy, the regions of a map become vertices, and the vertices become regions. In the example in the article, the red region in the central oval shares edges with the blue and the yellow regions on the right. In the graph, these regions become the red, blue and yellow vertices on the right of the picture. The edges of the graph each cross the corresponding edge of the map to join the vertices.

A simple graph and its dual.

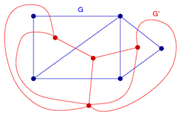The blue net G has $3$ regions $5$ vertices and $7$ edges. All the 'outside' edges of G border on a single infinite area. Its red dual G' has $4$ regions $4$ vertices and $7$ edges. The red vertex at the bottom of the picture represents the infinite external area for G. Similarly the blue vertex at the top of the picture represents the external area for G'. Both the original net and its dual obey Euler's Formula for networks $f + v - e = 1$ or $\text{regions} + \text{vertices} - \text{edges} = 1$

Duality is an equivalence relation. The dual of a dual is topologically equivalent to the original object. For example in the case of polyhedra, the distances may change but the relations between the faces, vertices and edges remain the same. The concept of duality was used to transform the map colouring problem into colouring vertices, and finds applications for example in power circuits, information flow, and in dealing with immigration/emigration problems.

6. Knots

Following the development of topology in the early 20th century, mathematicians began to develop an algebra for the classification of knots.

Knots are three-dimensional objects which can be easily made using lengths of cord (cord shoelaces are a convenient size). Just as Tait began, pupils can make up their own knots. It can soon be demonstrated that there are right-handed and left handed knots which cannot be transformed one into another.

	This is the simplest knot called an un-knot! If you make a closed loop of cord, and twist it in any way you like, it can always be un-twisted to return to a loop like this. This property defines the equivalence of knots.
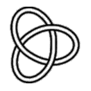	This knot is called a trefoil. It cannot be un-twisted to form a single closed loop.
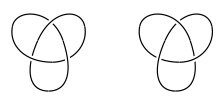	Here we have left-handed and right-handed trefoil knots. They are mirror images and cannot be manipulated one into another.

Good clear diagrams of knots can be found in the Rolfsen Knot Table at: http://katlas.math.toronto.edu/wiki/Image:Rolfsen_240.png

Knot theory is one of the most exciting fields of study in mathematics because of its many important applications in chemistry, pharmacy, biology and physics.

One area in which the left and right-handedness of molecules is very important is in the pharmaceutical industry. The drug Thalidomide was prescribed to pregnant women in the 1960s as a treatment for morning sickness. The drug did reduce morning sickness, but also caused horrible birth defects. The left-handed molecule was curing the sickness, but the right-handed molecule was causing severe damage to the foetus. Since this disaster, drug companies have had to be very careful about the effects of the mirror images of drug molecules.

More recently, the algebra associated with knot theory has found applications in particle physics. It's strange to think that Kelvin's vortex theory for atoms has eventually come full circle!