Copyright © University of Cambridge. All rights reserved.
'The Four Colour Theorem' printed from https://nrich.maths.org/
Show menu
The Four Colour Conjecture was first stated just over 150 years ago, and finally proved conclusively in 1976. It is an outstanding example of how old ideas combine with new discoveries and techniques in different fields of mathematics to provide new approaches to a problem. It is also an example of how an apparently simple problem was thought to be 'solved' but then became more complex, and it is the first spectacular example where a computer was involved in proving a mathematical theorem.
1. In the Beginning
The conjecture that any map could be coloured using only four colours first appeared in a letter from Augustus De Morgan (1806-1871), first professor of mathematics at the new University College London, to his friend William Rowan Hamilton (1805-1865) the famous Irish mathematician in 1852. It had been suggested to De Morgan by one of his students, Frederik Guthrie, on behalf of his elder brother Francis (who later became professor of mathematics at the University of Cape Town).


Augustus De Morgan (1807-1871) and William Rowan Hamilton (1805-1865)
The problem, so simply described, but so tantalizingly difficult to prove, caught the imagination of many mathematicians at the time. In the late 1860s De Morgan even took the problem and his proof to America where among others, Benjamin Peirce (1809-1880) a famous mathematician and astronomer, became interested in it as a way to develop his logical methods.
De Morgan used the fact that in a map with four regions, each touching the other three, one of them is completely enclosed by the others. Since he could not find a way of proving this, he used it as an axiom , the basis of his proof.
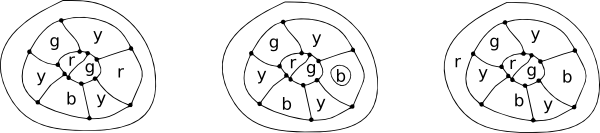
A copy of De Morgan's original sketch in his letter to Hamilton and a simple four colour map.
In 1878 Arthur Cayley (1821-1895) at a meeting of the London Mathematical Society asked whether anyone had found a solution for De Morgan's original question, but although there had been some interest, no one had made any significant progress. Cayley became interested in the problem and in 1879 published a short paper On the colouring of maps where he explained some of the difficulties in attempting a proof and made some important contributions to the way the problem was approached. His question that, 'if a particular map is already successfully coloured with four colours, and we add another area, can we still keep the same colouring?' began another line of enquiry which led to the application of mathematical induction to the problem.

Arthur Cayley (1821-1895)
Arthur Cayley showed that if four
colours had already been used to colour a map, and a new region was
added, it was not always possible to keep the original
colouring.
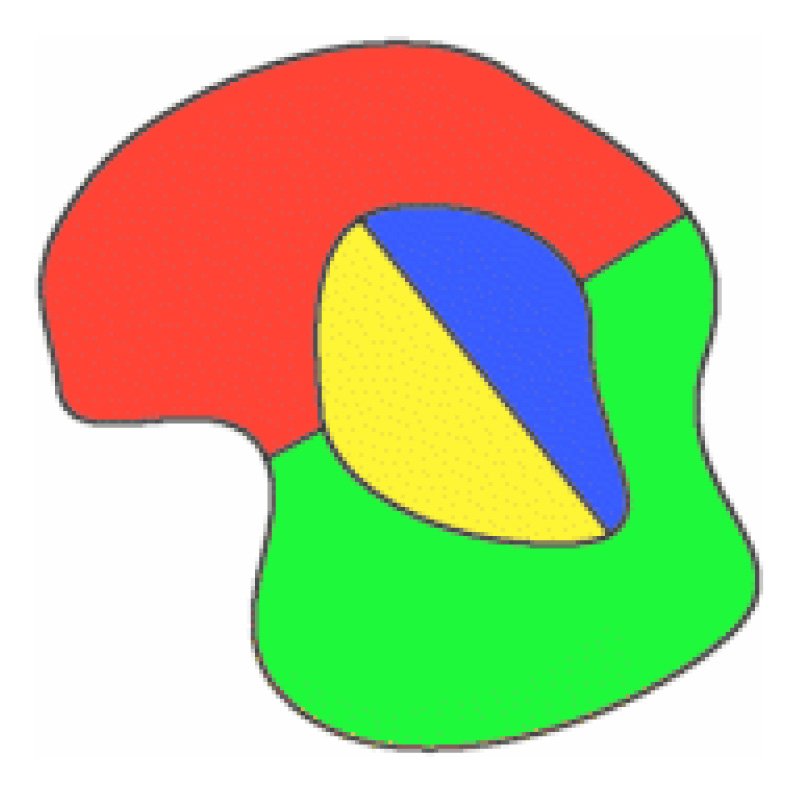
Above, all four colours have been used on the original map, and a
new region is drawn to surround it. In this case, a red region is
changed to blue, so that red can be used on the new surrounding
region.
Cayley also observed that it was possible to solve a version of the problem by restricting the way the boundaries met. For example, maps where just three countries met have three edges meeting at a vertex. These are called 'cubic maps', and the maps used in the following discussion are all cubic maps. Also, if a map can be coloured with four colours, only three colours will appear on the border.
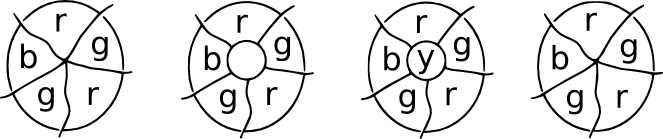
The Patch demonstration. Imagine that at some place in a map a number of countries meet at a point. Now put a patch over the meeting point, and all the new meeting points will have three borders emanating from them. These are cubic maps, and a fourth colour can be used for the central region. On removing the patch, we can return to the original colouring.
2. Some old techniques, new conditions and more problems!
In order to follow the developments of the problem, we need to investigate briefly some of the ideas, procedures and techniques that mathematicians developed in their attempts to solve it.
The Only Five Neighbours Conjecture [see note 1 below ]
'If you can't solve a particular problem, find an easier one that you can solve.' (Polya. How to Solve It )
'Every map has at least one country with five or fewer neighbours.'
Imagine a map of an island surrounded by the sea. In the colouring of the countries of the island, we count the sea as one region. Some countries may have only two borders (a digon), some three (as in a triangle), some four (a square) and some five (a pentagon) or more.
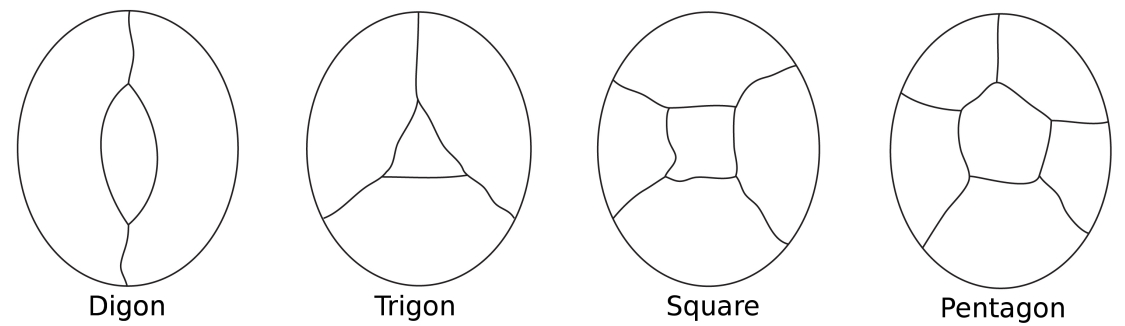
The simplest possible
configurations for surrounding a central region.
Note that in all of these configurations each node has only three
edges.
In 1813, Euler's formula for polyhedra was adapted for two dimensions by Augustin Cauchy (1759-1857) by projecting the polyhedron onto a plane thus forming the net of the solid. In this way the formula became $f + v - e = 1$, because Cauchy did not count the 'outside' region of the net.

Augustin Cauchy (1759-1857)
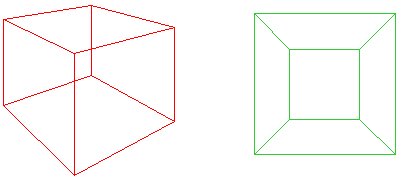
Imagine squashing the red cube down onto a plane so that its base is opened out to form the outside edge of the green net. Cauchy's idea was to cut out one face of the cube, so that for a plane polygon, $f + v - e = 1$. Alternatively, if the 'outside' of the net is regarded as a face with infinite area, then we still have $f + v - e = 2$
We can assume there are at least three border lines (edges) emerging from each meeting point (vertices).
So, from Euler's formula we get $3v$ edges in total. But, each edge has a vertex at the other end, and might be counted twice, so the total number of edges is at least $\frac{3}{2} v$. So $e \geq\frac{3}{2}v$ or, $v \leq \frac{2}{3}e$.
The proof that the map has at least one country surrounded by five or fewer neighbours proceeds by contradiction . If this leads to an absurdity, we have a proof.
Assume there is a map where every country ($f$) is surrounded by at least six neighbours. If we select one country, and count all the border lines ($e$) of the countries surrounding that one, we have six borders. This will occur for all the countries in the map, so the total number of borders will be $6f$ (where $f$ is the total number of countries in the map). However, each border line has been counted twice, so we need $\frac{6}{2}f$ which means $e \geq3f$ or $f \leq\frac{1}{3}e$.
Now put these values into Euler's formula: $$f + v - e = 2$$ and we have $$1/3(e) + 2/3(e) - e$$ which is zero!
This is the absurdity, so our original assumption was false. This means that there must be at least one country with five or fewer neighbours!
Minimal Criminals!
Another way to tackle the four colour problem is to assume it is false, and see where this leads. Suppose there are maps that need five colours or more, and we pick the maps with the smallest possible number of countries. These maps are called minimal counter-examples or minimal criminals !
So this means that a minimal criminal cannot be coloured with four colours, but any map with fewer countries can be coloured with four colours. If we can show that minimal criminals cannot exist, then we might be able to make some progress.
For example, we can show that a minimal criminal cannot contain a digon.
From the original map, take away a boundary from the digon, and we get a new map with fewer countries. This map can be coloured with four colours (from our assumption). We then colour this new map, (we only need two colours). Now replace the border we removed, and re-colour the map. We have used three colours, and since there is still one more colour available, this shows that our map can be coloured with four colours. But this is against our assumption, so a minimal criminal cannot contain a digon.
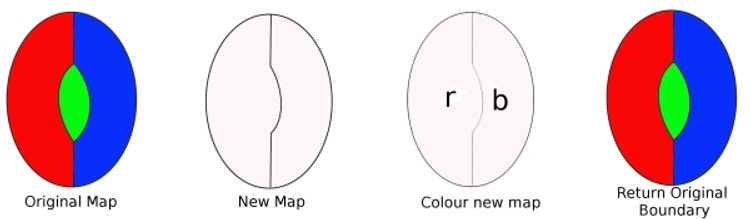
To show that a Minimal Criminal cannot contain a region with two edges (a digon). Suppose there is a minimal criminal that contains a digon. Removing an edge means the map contains fewer regions. So this new map can be coloured with four colours. Now replace the lost edge. Since only two colours were needed before, replacing the edge means we can use a third colour, and still have a fourth colour to use. So, a minimal criminal can be coloured with four colours. Hence a minimal criminal cannot contain a digon.
This procedure can be repeated to show that a minimal criminal cannot contain a three-sided country (a trigon), but it breaks down when we try the technique on a square, because when we replace the square, the countries next to it may well be using all four colours, so the proof procedure fails. Once this has happened, it becomes obvious it won't work for pentagons, and so on.
The Six Colour Theorem
A similar technique can be applied to show that the six colour theorem is true. First, we assume there are no maps that can be coloured with six colours. Some of the maps can be coloured with seven colours, so selecting one of these (a minimal criminal), if we can show that it is possible to colour it with less than seven colours, we have achieved our aim.
From the proof of the five neighbours theorem, it is possible to proceed using the minimal criminal idea to show that any map can be coloured with six colours!
3. From Regions to Knots, Networks and Topology
In 1879 Alfred Kempe (1849-1922), using techniques similar to those described above, started from the 'five neighbours property' and developed a procedure known as the method of 'Kempe Chains' to find a proof of the Four Colour Theorem. He published this proof in the American Journal of Mathematics. He found two simpler versions that were published in the next year, and his proof stood for ten years before Percy Heawood (1861-1955) showed there was an important error in the proof-method that Kempe had used.


Alfred Kempe (1849-1922), Peter Guthrie Tait (1831-1901) and Percy Heawood (1861-1955)
In 1880 P.G. Tait (1831-1901) a mathematical physicist, offered a solution to the problem. Independently, Tait had established that maps where an even number of boundary lines meet at every point, could be coloured with two colours, although this result had appeared earlier in Kempe's papers.
During 1876-77 Tait became well-known for his study and classification of knots. At that time there were a number of different theories about the structure of atoms. William Thompson (Later, Lord Kelvin 1824-1907) inspired by the experiments of the German Physicist Hermann von Helmholtz (1821-1894) proposed a theory that atoms were knotted tubes of ether. Kelvin's theory of 'vortex atoms' was taken seriously for about twenty years, and it inspired Tait to undertake a classification of knots. Tait, Thomson and James Clark Maxwell (1831-1879) invented many topological ideas during their studies. However, Kelvin's theory was fundamentally mistaken and physicists lost interest in Tait's work.[see note 2 below ]


Hermann von Helmholtz (1821-1879), Lord Kelvin (1824-1907) and James Clark Maxwell (1831-1879)

Tait began with the ways in which a single closed loop of cord could be knotted. He had no systematic method at the start, and began in an intuitive way by taking a single closed loop and experimenting with the ways in which it could be knotted. Of course, the cord had to be open (like a shoelace) then knotted, and joined. Note that if you follow the cord around the knot, the 'over - under' crossings will alternate. He then went on to experiment with two loops and the ways in which they could be knotted together. Shown here are knots with up to six crossings for a single loop.
One of the outcomes of Tait's study was his Hamiltonian graph conjecture.
A map is regarded as a polyhedron drawn on a sphere, and it can then be projected onto a plane. Tait proposed that any cubic polyhedral map has a Hamiltonian cycle [see note 3 below ]. Tait's method focused on the edges of the graph and he showed that a Hamiltonian cycle could produce a four-coloring of a map. It was not until 1946 that William Tutte (1917-2002) found the first counterexample to Tait's conjecture.
Tait and the connection with knots
Tait initiated the study of snarks in 1880, when he proved that the four colour theorem was equivalent to the statement that no snark is planar. A planar graph is one that can be drawn in the plane with no edges crossing. It looks as if Tait's idea of non-planar graphs might have come from his study of knots and Hamiltonian paths .
The first known snark was the Petersen graph discovered in 1898, and mathematicians began to hunt for more of these kinds of graphs but it was not until 1946 that another snark was found.
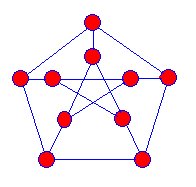 |
Snarks are projections of three dimensional graphs onto the plane. There are no vertices where the blue edges appear to cross each other. Snarks have the following properties:
|
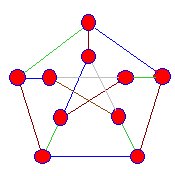 |
The edges meeting the vertices of this snark are coloured blue, green and brown, but we always reach a stage where this process cannot be continued. |
Julius Peterson (1839-1910)
The Hunting of the Snark is a poem written by Lewis Carroll, and Martin Gardner named these graphs Snarks, because they were so elusive.
4. Transforming the problem and finding new methods.
Although Heawood found the major flaw in Kempe's proof method in 1890, he was unable to go on to prove the four colour theorem, but he made a significant breakthrough and proved conclusively that all maps could be coloured with five colours.
Heawood made many important contributions to the problem, shifting the focus of attention from the areas of a map, to the borders between them. By 1898 he had proved that if the number of edges around each region is divisible by 3 then the regions could be coloured with four colours.
Cauchy's proof of Euler's formula also included the idea that any net of a polyhedron can be triangulated by adding edges to make non-triangular faces into triangles. He then developed a procedure whereby he deleted the edges one by one, showing that Euler's formula could be maintained at each step.[see note 4 below ]
Cauchy's Proof of Euler's Formula
Cauchy's 1813 proof of Euler's Formula began with the idea of a projection of a polyhedron to obtain a plane net. He further demonstrated (a) that any net could be triangulated, and his proof (b) of Euler's Formula was accepted at the time.
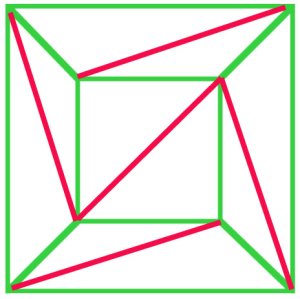 (a)
|
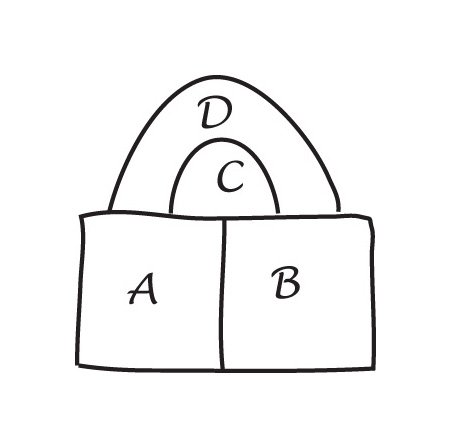
In principle, every polygonal net can be triangulated. In this net of a cube (a), $f + v - e$ is $10 + 8 - 17 = 1$, and Euler's formula still holds. |
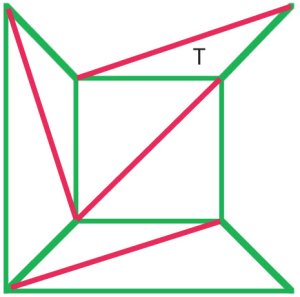 (b)
|
Cauchy's argument was to remove the external edges from diagram (a) one by one, and when he reached a stage as in diagram (b) removed the whole triangle T, thus preserving Euler's formula. Many mathematicians of the early nineteenth century agreed that this procedure demonstrated a proof of Euler's formula for all polyhedra. |
By 1900, mathematicians knew that a planar graph can be constructed from any map using the powerful concept of duality [see note 5 below ]. In the dual, the regions are represented by vertices and two vertices are joined by an edge if the regions are adjacent. In these graphs, the Four Colour Conjecture now asks if the vertices of the graph can be coloured with 4 colours so that no two adjacent vertices are the same colour.
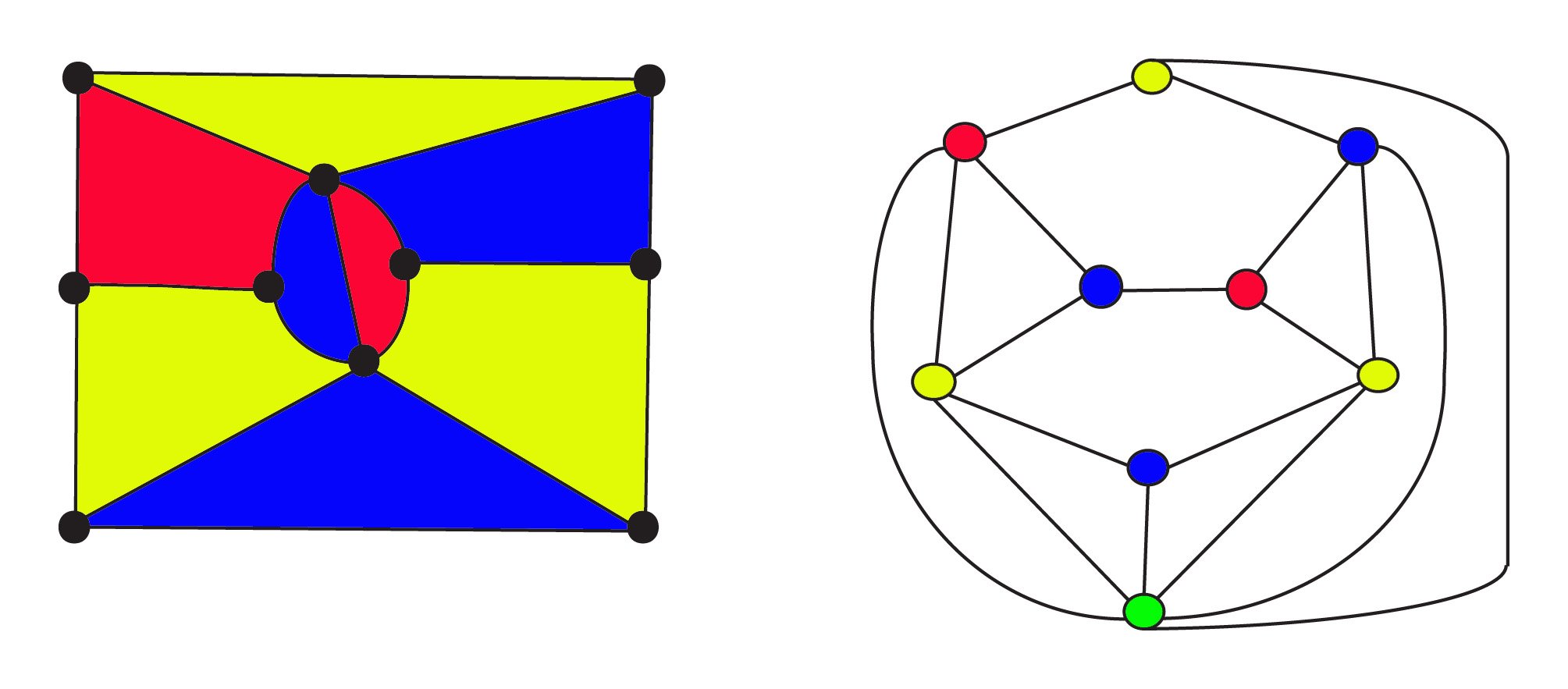
The 3-coloured map on the left has $8$ regions $10$ vertices and $17$ edges. Its dual graph on the right has $9$ regions $9$ vertices and $17$ edges where the vertices are coloured the same as the areas of the map. The green vertex at the bottom of the graph represents the infinite external area for the map. Both the original map and its dual obey Euler's Formula for networks $f + v - e = 1$ or, $\text{regions} + \text{vertices} - \text{edges} = 1$. The duality relation is symmetric: the dual of the dual will be the original graph, where regions and vertices are exchanged.
During the first half of the twentieth century, mathematicians focused on modifying these kinds of techniques to reduce complicated maps to special cases which could be identified and classified, to investigate their particular properties and developed the idea of a minimal set of map configurations that could be tested.
In the first instance, the set was thought to contain nearly 9,000 members which was an enormous task, and so the mathematicians turned to computer techniques to write algorithms that could do the testing for them. The algorithms used modified versions of Kempe's original idea of chains together with other techniques to reduce the number of members of the minimal set.
After collaborating with John Koch on the problem of reducibility, in 1976 at the University of Illinois, Kenneth Appel and Wolfgang Haken eventually reduced the testing problem to an unavoidable set with 1,936 configurations, and a complete solution to the Four Colour Conjecture was achieved. This problem of checking the reducibility of the maps one by one was double checked with different programs and different computers. Their proof showed that at least one map with the smallest possible number of regions requiring five colours cannot exist.
Since the first proof, more efficient algorithms have been found for 4-coloring maps and by 1994, the unavoidable set of configurations had been reduced to 633.
Is a 'Proof' Done on a Computer a Proper Proof?
Because the proof was done with the aid of a computer, there was an immediate outcry. Many mathematicians and philosophers claimed that the proof was not legitimate. Some said that proofs should only be 'proved' by people, not machines, while others, of a more practical mind questioned the reliability of both the algorithms and the ability of the machines to carry them out without error. However, many of the proofs written by mathematicians have been found to be faulty, so the argument about reliability seems empty. Whatever the opinions expressed, the situation produced a serious discussion about the nature of proof which still continues today.
For pedagogical notes:
Use the notes tab at the top of this article or click here .
Notes
- More detail of this and the other procedures found in this section can be seen in Robin Wilson's book Four Colours Suffice .
- Knots can be left-handed or right-handed, and today there are important applications of this property in chemistry, pharmacy, biology and physics. (See Pedagogical Notes)
- Named after William Rowan Hamilton (1805-1865). A Hamiltonian path in a graph visits each vertex exactly once. A Hamiltonian cycle (or circuit) is a path which visits each vertex exactly once and returns to the starting vertex.(See Pedagogical Notes)
- The book by Imre Lakatos, Proofs and Refutations has a discussion and criticism of Cauchy's procedure (pages 6 - 12), and much more on the story of Euler's Theorem.
- The idea of duality arose in the 16th and 17th centuries with developments in projective geometry. Mathematicians like Pascal and Desargues found that new theorems could be found by exchanging the terms 'point' and 'line' in descriptions of certain geometrical configurations. An example is in regular polyhedra, where the vertices of one correspond to the faces of the other. So the dual of a tetrahedron is another tetrahedron, and the dual of a cube is an octahedron. The dual of the dual is the original polyhedron.
References
The very best popular, easy to read book on the Four Colour
Theorem is:
Wilson, R. (2003)
Four Colours Suffice
.
London. Penguin Books.
For a more detailed and technical history, the standard
reference book is:
Biggs, N.; Lloyd, E. & Wilson, R. (1986) (1998)
Graph Theory,
1736-1936
Oxford. Oxford University Press.
This one brings us up to date, with more recent foundations and
philosophy.
Fritsch, R and Fritsch, G (2000)
The Four Color Theorem: History,
Topological Foundations, and Idea of Proof
New York. Springer-Verlag.
Hardly any general history book has much on the subject, but the last chapter in Katz called 'Computers and Applications' has a section on Graph Theory, and the Four Colour Theorem is mentioned twice.
Polya G. How to Solve
It.
This is the classic book about Problem Solving. There have been
many editions of this book since it first appeared in the 1950s and
it is still easily available. Curiously, recent editions have been
given the subtitle 'A new aspect of Mathematical Method'.
Lakatos, I. (1976) Proofs and
Refutations: The Logic of Mathematical Discovery.
Cambridge. C.U.P.
This is another important book which led to the research into
Problem Solving and Investigations in the 1970s. It begins as a
classroom discussion between a teacher and a group of students
about the proof of Euler's formula, and ranges through the ideas,
objections and possibilities that were actually discussed by
mathematicians and scientists in the nineteenth century. It raises
some of the most important issues about teaching and learning
problem solving and about mathematical methods and proof.
Related References
I have had a little book on String Games for some time. When I was at school it was called Cat's Cradle, and we played it in our break time.
Recently, a French journal has published a paper on the 'algebra' of string figures! If you go to Amazon you will find a nice book by Ann Swain and Michael Taylor called Finger Strings: A Book of Cats Cradles and String Figures to be published by Floris books in September 2008. There are some 80 figures described with coloured diagrams. It's spiral bound, so it will stay open while you follow the instructions. It also comes with a couple of string loops!
For knot experts, The Ashley Book of Knots is a classic for anyone interested in the hundreds of different kinds of knots and their uses. Amazon has various editions available at different prices.
Web Links
For a general overview and links to many people and topics, the
MacTutor website is
http://www-history.mcs.st-and.ac.uk/HistTopics/The_four_colour_theorem.html
And of course MacTutor biographies of those involved in developing all the different mathematical aspects can be found at the MacTutor Biographies Index.
The Four Colour Theorem and Three Proofs. For the mathematically persistent the following website has an intriguing new approach to attacking the problem of constructing a new algorithm for solving the problem, and tying to reduce the reliance on a computer. http://www.emu.edu.tr/~cahit/the%20four%20color%20theorem%20---%20three%20proofs.htm
For Graph Theory, Wikipedia gives a good overview, and you can
skip the really technical stuff. It shows the kinds of modern
applications of this area of mathematics. If you go to Graph
Colouring and click on the Four Colour Theorem, then you will find
a lot more information.
http://en.wikipedia.org/wiki/Graph_theory
An interesting, and not too technical History of Knot Theory -
how an idea from Kelvin's Physics returns to Atomic Theory
today.
http://www.math.buffalo.edu/~menasco/Knottheory.html
The Association of Teachers of Mathematics have Celtic Knot
design posters. Go to their website and browse the alphabetical
list of resources.
http://www.atm.org.uk/
Find out all about Knots on the Knot Atlas! If you are not an
expert - just enjoy the variety and complexity of the database "in
the spirit of wiki"
http://katlas.math.toronto.edu/wiki/Main_Page
More artistic and colourful - but no less mathematical is the
Knot Plot Site.
http://www.knotplot.com
For those who want some of the original stuff and historical
detail go to the History of Knot Theory on:
http://www.maths.ed.ac.uk/~aar/knots/index.htm