Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Treasure Hunt
- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Ci Hui Minh Ngoc Ong from Kelvin Grove State College (Brisbane) in Australia, Uday from England and Asiya all sent in their strategies for level 1. This is Uday’s strategy:
You must start in the middle (6,6) as the middle is equally as close to all four of the corners. Then if the treasure is more than (I used this rule, you don't have to use these exact same numbers) 4 steps away, then you go for (any) one of the corners and you input the coordinates right in between the center and the corner you chose. If it's further away than when you did (6,6) go for the midpoint of the center and the opposite corner. Keep doing this until you get close (less than 6 steps away) then you find every possible coordinate it could be but don't enter it yet, click on them and then count if they are the number away from the points previously plotted as it say on the points. When you find one which is correct and you've checked it with all of the points previously plotted, enter it.
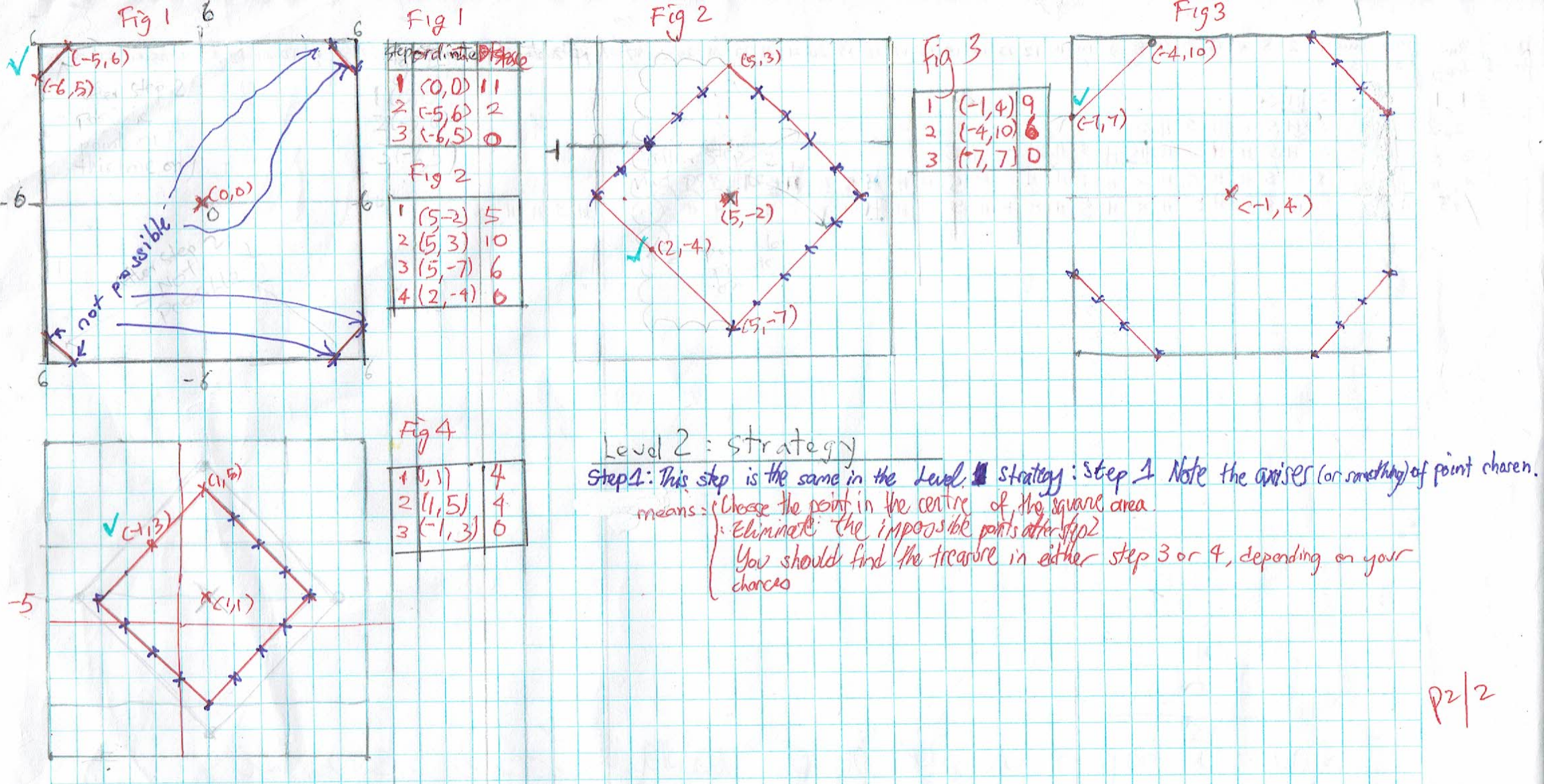
Asiya and Ci Hui Minh Ngoc Ong had the same strategy. This is Asiya’s description with Ci Hui Minh Ngoc Ong’s diagrams:
Firstly, I’d choose the spot most close to the centre, this was because I’d have the most space to plot the points around. after making my first guess I plotted all the possible points and realised it made a symmetrical diamond shape, the length and height being the closest possible steps given, I then chose one of the point in the diamond shape and repeat the process, which gives me only two possible overlapping points. I’d guess either of these points completing it usually under 4 guesses.
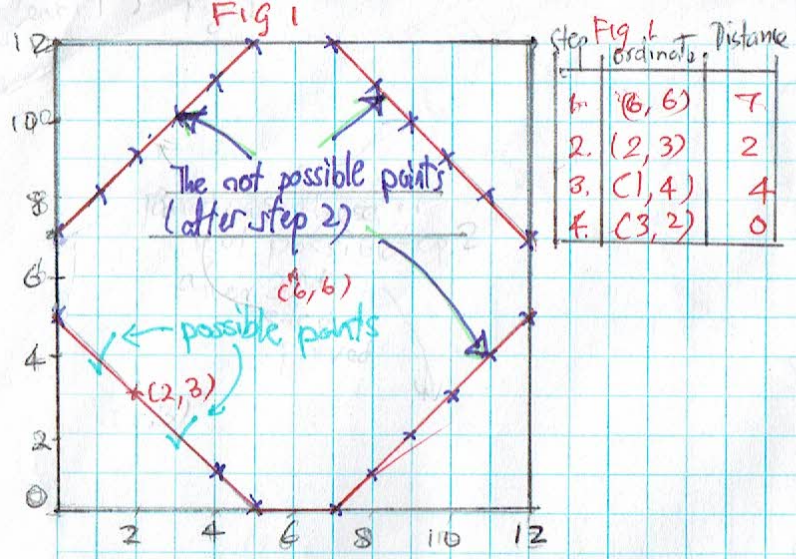
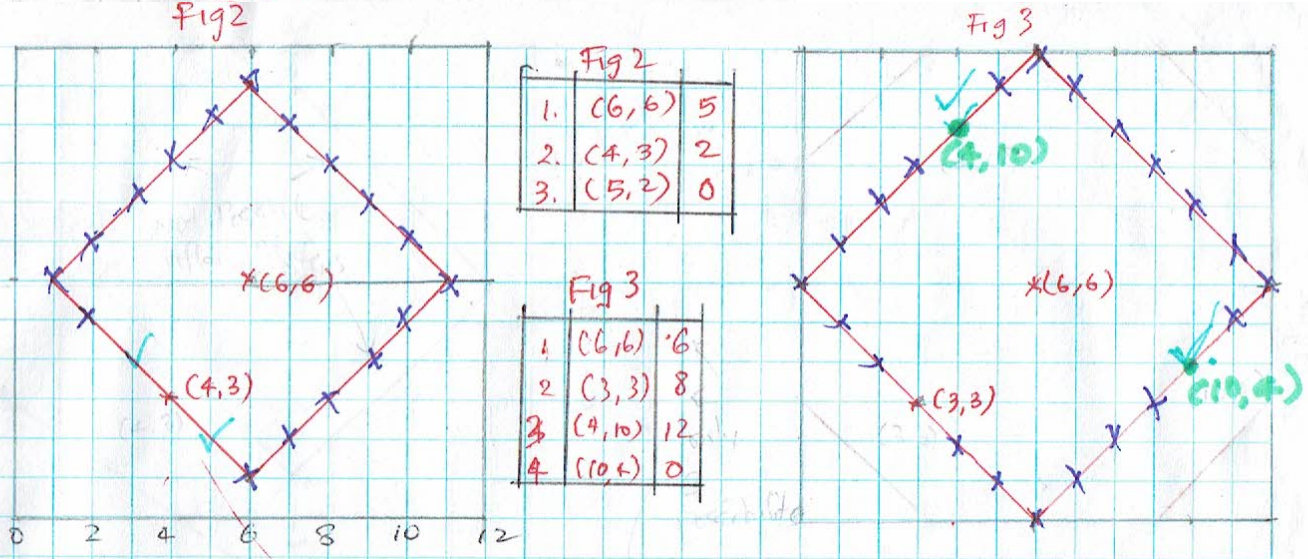
Ci Hui Minh Ngoc Ong also sent in a strategy for level 2 (click on the image to see a larger version):
This is Aisha’s strategy for level 3:
For level 3 I did the same, however instead of the middle of the graph I’d do it in the middle of the pink space. Creating the diamond shape around id guess two other spaces usually farther from the centre and plot around it which would leave me one point
Elijah and his mum worked out a strategy for level 4:
First of all we had to work out how to think about this problem. My mum worked it out. She tried drawing 3d pictures on squared paper, and then on isometric paper, but they were both too confusing. Then she remembered games of 3d chess and 3d noughts and crosses and so she drew ten 9x9 grids, and labelled them z=0 up to z=9.
First guess: (0, 0, 0) I marked all the possible points that were the right distance away - these came out as diagonal lines on the grids. (Don't have to be on each of the ten grids.)
Second guess: (9, 0, 0) I used this one because it was the same as the second guess from Level 1. Marked all the possible points again, which gave diagonal lines going the other way, so where they crossed gave some possible hiding places.
Third guess: we took a few goes to work out what was the best point to use for our third guess. We wanted to use another corner of the cube, but our first couple of tries gave us sets of points that we had already got from our first two guesses. We decided on (0, 0, 9) Marked the possible points again, and that gave only one possible hiding place.
Fourth guess: The treasure!