Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Trominoes
Age 11 to 16
Challenge Level 





A tromino is a $3 \times 1$ block:

What sized rectangles may be made using trominoes? You can print off and cut out trominoes from this sheet . Alternatively, if you have a set of the game Jenga, then use the blocks as trominoes (but check they are $3 \times 1$ first)
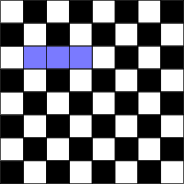
Can you cover $63$ squares of an $8\times 8$ chessboard using trominoes? (Why can't you cover $64$?). If so, which square remains uncovered, and are there other arrangements of the trominoes which would lead to a different square being left uncovered?
Think of some other squares which cannot be covered with trominoes. Can you "almost" cover them, leaving only one hole? When can an $n \times n$ square be covered or "almost" covered?