In Nyeong Chang sent us the solution to the two divisions set in the problem, set out using Galley Division, and explained a little about how it works:


Not only are the answers same as when the long division method was applied, but the same numbers are appearing. This works because the basic mechanism of division is the same. What is done in both long division and Galley division is seeing how many of the divisor can fit into the dividend one digit at a time, and then calculating the remaining number, and repeating until a remainder smaller than the divisor is left.

Mao Yamamoto worked out $76254 \div 35$ rather than $235$ but showed very nicely how the standard long division method relates to the Galley Division method by setting out the Galley Division in the same way:

The method works in the same way as our modern methods of division. The only difference is that when the denominator is more than one digit and subtraction is needed, denominators are separated as one digit and calculated. For example, in the calculation $76254 \div 35$ below, in the modern method we need to multiply $35$ by $2$ and subtract from $76$. In Galley division, we multiply $3$ by $2$ and subtract from $7$. Then we multiply $5$ by $2$ and subtract from $16$.

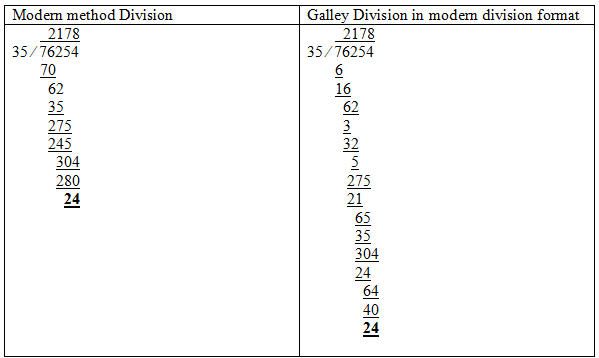
Compared with the modern methods of division, this Galley Division may be easier for some students as it allows them to subtract numbers with fewer digits.