 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Coins on a Plate



- Problem
- Student Solutions
Here we use excerpts from several different proofs.
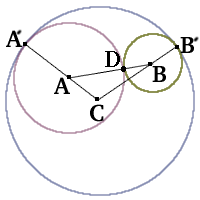
We start with the solution fromMolly and Catherine of Mount School, York .
Points C, A and A' are co-linear. To explain this, consider the common tangent to both circles at the point of contact. It is both perpendicular to CA' and to AA' so, as there is a common point in A' , the initial statement is demonstrated.
Molly and Catherine's method proves, in the same way, that C, B and B' are co-linear and A, D and B are co-linear. They finished the proof correctly as did Sarah and Caroline of Ipswich High School and James of Hethersett School, Norfolk. For the following method you may visualise swinging AD round to AA' and BD round to BB'.
Next is the solution byCharlotte and Frances of Ipswich High School
It can be proved that the triangle ABC has perimeter equal to the diameter of the circle centre C because AD = AA' making CAD = CAA' and BD = BB'
so CBD = CBB' . This proves that the perimeter of the triangle ADBCA equals the diameter of the circle because CAA' and CBB' are both radii.
Clare of Maidstone Girls' Grammar School used much the same method as Charlotte and Frances.