Triangle in a hexagon

Call the length of one side of the hexagon $s$ and the height of the hexagon $h$:



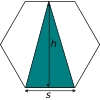
So the area of the shaded triangle is $$\frac{1}{2}\times s\times h$$

Now divide the hexagon into $6$ equilateral triangles:



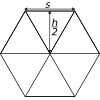
Each triangle has area $$\frac{1}{2}\times s\times \frac{h}{2}$$ so the area of the hexagon is $$6\times \frac{1}{2}\times s\times \frac{h}{2}=3\times \frac{1}{2}\times s\times h$$ or $$3\times \text{Shaded area}$$

So the shaded area is $\frac{1}{3}$ of the area of the whole hexagon.