Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Distinct in a Line
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
$3$, $4$ and $5$ are on diagonals, so can't go in the centre square (since each number must appear just once on each diagonal).
So the number in the centre square must be a $1$ or a $2$. Suppose it was a $1$. Then we must put $1$s as shown in red:
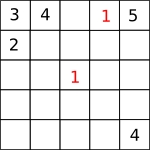
and $2$s as shown in blue:
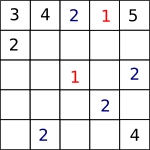
So there must be a $1$ in place of one of the crosses:
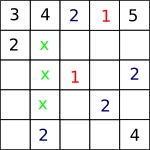
But the top and bottom cross couldn't be $1$, since they are on the diagonal, and the middle cross can't be $1$ since it's on the $3$rd row (where there's already a $1$). So $1$ can't go in the centre square after all!
$2$ goes in the centre square.
Alternatively, consider the bottom-left corner. $2$ and $3$ are in the same column, $4$ is in the same row and $5$ is in the same diagonal. Therefore, this must contain a $1$.
Then, the centre is in the same diagonal as each of the corners, so cannot be $1$, $3$, $4$ or $5$. This means the centre must contain a $2$.
So the number in the centre square must be a $1$ or a $2$. Suppose it was a $1$. Then we must put $1$s as shown in red:

and $2$s as shown in blue:

So there must be a $1$ in place of one of the crosses:

But the top and bottom cross couldn't be $1$, since they are on the diagonal, and the middle cross can't be $1$ since it's on the $3$rd row (where there's already a $1$). So $1$ can't go in the centre square after all!
$2$ goes in the centre square.
Alternatively, consider the bottom-left corner. $2$ and $3$ are in the same column, $4$ is in the same row and $5$ is in the same diagonal. Therefore, this must contain a $1$.
Then, the centre is in the same diagonal as each of the corners, so cannot be $1$, $3$, $4$ or $5$. This means the centre must contain a $2$.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.