 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Griddy Region



- Problem
- Solutions
$$\frac{11}{12} \; \text{square units}$$
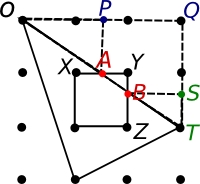
We want to find out how far the points $A$ and $B$ (the points on both the triangle and square) are from $Y$. The triangle $OQT$ is $3$ units across by $2$ units down. The triangle $OPA$ is similar to $OQT$, and is half its size (since it is one unit down rather than two). So the point $A$ is $\frac{3}{2}$ units from $O$, so $\frac{3}{2}-1=\frac{1}{2}$ unit from $X$, so
$1-\frac{1}{2}=\frac{1}{2}$ unit from $Y$
Similarly, the triangle $BST$ is $\frac{1}{3}$ the size of $OQT$, so the point $B$ is $\frac{2}{3}$ unit from $Z$, so $1-\frac{2}{3}=\frac{1}{3}$ unit from $Y$. So the triangle $AYB$ has area $$\frac{1}{2}\times \frac{1}{2}\times \frac{1}{3} \; \text{square units}= \frac{1}{12}\; \text{square units}$$ so the area of the overlap is $$1-\frac{1}{12}\; \text{square units}=\frac{11}{12}\;
\text{square units}$$