Copyright © University of Cambridge. All rights reserved.
'Cutting Corners' printed from https://nrich.maths.org/
Show menu
Why do this problem?
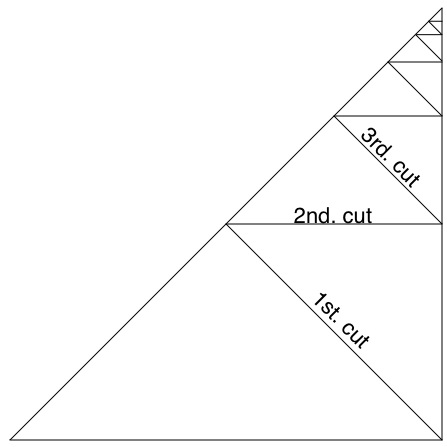
This is such an open investigation - I really feel that it is good, every now and again, to include such an activity as this in the children's mathematical experience. The pupils' understanding of the properties of these isosceles triangles will be enhanced. The concept of area is often challenged in this
investigation as our eyes seem to play tricks on us and we have to verify things in a more certain way. With some pupils you may even start thinking about Pythagoras and square numbers and square roots.
Possible approach
You'll need to be enthusiastic in a way that will capture the pupils' interest and imagination. You could begin by working on the board and demonstrating how to cut the triangle in half (turning it on its side helps to see the symmetry for some children). Then offer the children a large ready-made triangle each for them to halve and halve again. If you use different coloured paper for
each child then you might encourage them to swap a piece of the same size and shape with a another child, so making their pattern more interesting.
Key questions
Do you notice anything about the pattern/shape you've made?
Can you make other shapes with the triangles you've chosen to use?
Possible extension
Is it possible to halve all triangles like this? Why or why not?
Possible support
It may be necessary to help those who lack confidence in manipulation to draw lines with a ruler and cut the triangles. You might prefer to draw lines ready to cut, and focus the activity instead on the language of shape and size.