 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Cutting Corners



I don't know about you but when I'm walking or cycling I like to cut a corner if it's possible and safe. I do this most when I'm walking along a path and the next path is a long way ahead and going off to the left at right angles. Looking from above this might look like this :-

and so I decide to "cut the corner" as it saves time, it's a shorter distance to go, and you can overtake someone who is walking around the path. So I go along the dotted route.

Hey this makes a rather good triangle, also, I guess, rather special. The two shorter sides are the same length and are at right angles to each other.
You may, at school, have a collection of these kinds of triangles and you might be able put them together in different kinds of designs and patterns.

I thought it would be good to have a very "OPEN" challenge this time since this triangle came from the open-air! Here it is drawn on its own.

I've taken a big one of these triangles and cut it several times in a special way. The first cut was from the bottom right hand corner and cut the big triangle in half. I've then gone on to cut in a "Zig-Zag" fashion each cut halves the previous triangle, each time halving the remaining triangle.
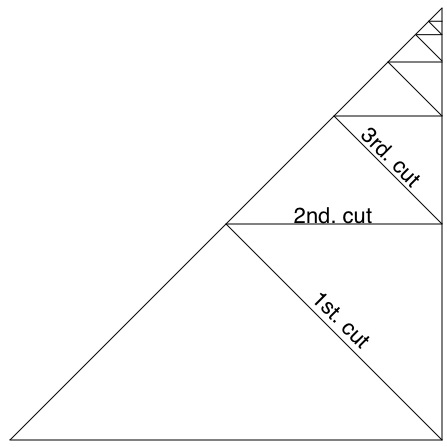
These cuts give us lots of triangles and my challenge to you, by using many of these triangles is to come up with the MOST,
the MOST Extraordinary,
the MOST AMAZING,
the MOST UNUSUAL,
the MOST . . . . . . !? PATTERNS/DESIGNS
You might do it on paper or card. But you might be able to use a draw program on your computer to make these Triangles [if you do that make sure that they are half of the size of the last one].
Finally - - as always -- "I wonder what would happen if we were allowed to . . . . ?"