 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Isosceles



- Problem
- Student Solutions
From the diagram sent in by Chin Siang, Tao Nan School, Singapore, you can see that triangles AEG and BDI are equal in area because each is made up of two right angles triangles with sides 3, 4 and 5 units with the line IC as an axis of symmetry:
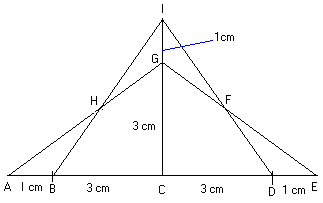
Suzanne and Bethany (the Mount School, York) sent us this solution:
Any isosceles triangle with base b , height h and area bh /2 can be split into two right angled triangles along the axis of symmetry and these right angled triangles can be re-assembled into a second isosceles triangle with base 2 h , height b /2 and area bh /2. The only case in which the pair of isosceles triangles are congruent is where b = 2 h so there are infinitely many pairs of non congruent isosceles triangles with the same area. In general the sides are not of integer length but there are also infinitely many such pairs with sides of integer length formed from right angled in which the lengths of the sides are Pythagorean triples. For example the two isosceles triangles with sides 13,13, and 10 units and with sides 13,13, and 24 units both have area 60 square units.
The Pythagorean triple 7, 24, 25 gives triangles with sides 25, 25, 14 and 25, 25, 48 which both have areas of 168 square units, and we can go on doing this with Pythagorean triples of which there are lots. As for isosceles triangles with an area of 12 square units, well it only needs the base and height to have a product of 24, so, if we insist on whole numbered sides, then there are only two - the ones given. If sides do not have to be whole numbers then there are an infinite number of solutions, though some would be difficult to tell apart.
You may also like
The Old Goats
A rectangular field has two posts with a ring on top of each post. There are two quarrelsome goats and plenty of ropes which you can tie to their collars. How can you secure them so they can't fight each other but can reach every corner of the field?
Trice
ABCDEFGH is a 3 by 3 by 3 cube. Point P is 1/3 along AB (that is AP : PB = 1 : 2), point Q is 1/3 along GH and point R is 1/3 along ED. What is the area of the triangle PQR?