Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
pH Temperature
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
The initial key to this problem is to realise that for self-dissociating water, [H]$^+$ = [OH]$^-$.
Therefore, K$_W = [H^+]^2$
Since pH = $-log_{10}[H^+]$
$\mathbf{\Rightarrow K_W = 10^{-2pH}}$
When pH = 7; $K_W = 1 \times 10^{-14}$
pH =6.8; $K_W = 2.51 \times 10^{-14}$
pH = 7.2; $K_W = 0.398 \times 10^{-14}$
Plotting a graph of $K_W$ versus temperature gives:
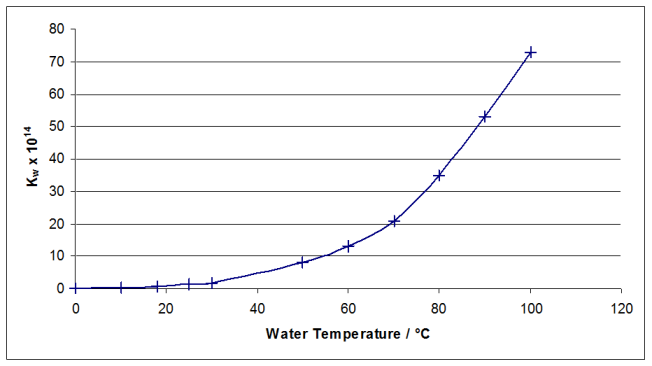
By drawing a smooth curve of best fit through the points, the relevant temperatures can be read off the graph for the given values of $K_W$. If you draw the graph for the entire temperature range, it is difficult to read off accurate values in the required range, which are all smaller than $10\times 10^{14}$. Plotting the curve through the first three points allows us to read off accurate values.