 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Dilution Series Calculator



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
A solution to an interactive of this sort is best done with a
worked example:
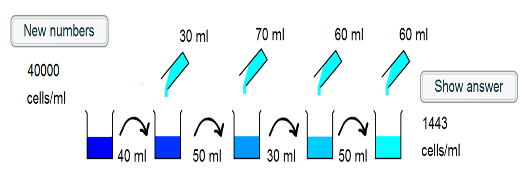
1) The intial beaker contains 40000 cells/ml. 40ml of this is
taken, and so there are $40000 \times 40 = 1.6 \times 10^6$ cells
placed into the second beaker.
2) 30ml of water is added to the second beaker, such that the
cells are in a volume of 70ml. The concentration is now $\frac{1.6
\times 10^6}{70} =2.29 \times 10^4$ cells/ml.
3) 50ml of this suspension is taken and placed into the third
beaker, and so $2.29 \times 10^4 \times 50 = 1.14 \times 10^6$
cells are transferred.
4) A further 70ml of water is added, such that the cells are in a
120ml suspension. This corresponds to a concentration of
$\frac{1.14 \times 10^6}{120} = 9.52 \times 10^3$ cells/ml.
5) 30ml of the suspension is transferred, which corresponds to $30
\times 9.52 \times 10^3 = 2.86 \times 10^5$ cells.
6) 60ml is added to the fourth beaker, and so the cells are in a
90ml volume. The concentration is hence $\frac {2.86 \times
10^5}{90} = 3175$ cells/ml.
7)50ml of the suspension is transferred to the final beaker,
corresponding to $ 50 \times 3175 = 1.59 \times 10^5$ cells
8) 60ml more water is added to give a final volume of 110ml. Thus
the final concentration is $\frac{1.59 \times 10^5}{110} = 1443$
cells/ml
Of additional interest is a general rule.
$n_f$ is the final cell concentration
$n_i$ is the initial cell concentration
$V_1, V_2, V_3, V_4$ are the volumes transferred to the second,
third, fourth and fifth beakers respectively
$V_a, V_b, V_c, V_d$ are the volumes added to the second, third,
fourth and fifth beakers respectively.
Thus,
$$n_f = \left(\frac{\left(\frac{\left(\frac{\left(\frac{n_i \times
V_1}{V_1 +V_a}\right) \times V_2}{V_2 + V_b}\right) \times V_3}{V_3
+ V_c}\right)\times V_4}{V_4 + V_d}\right)$$
$$ = \frac{n_iV_1V_2V_3V_4}{(V_1 + V_a)(V_2 + V_b)(V_3 + V_c)(V_4
+ V_d)}$$
Thus, the dilution series calculation reduces to multiplication of
fractions.
You may also like
Golden Thoughts
Rectangle PQRS has X and Y on the edges. Triangles PQY, YRX and XSP have equal areas. Prove X and Y divide the sides of PQRS in the golden ratio.
At a Glance
The area of a regular pentagon looks about twice as a big as the pentangle star drawn within it. Is it?
Contact
A circular plate rolls in contact with the sides of a rectangular tray. How much of its circumference comes into contact with the sides of the tray when it rolls around one circuit?