From a random world to a rational universe
Randomness, Luck, Astragali and Dice
In the time before the mathematical idea of randomness was discovered, people thought that everything that happened was part of the will of supernatural beings, the gods, who looked down upon human affairs and decided to 'tip the balance' one way or another to influence events. Hence, sacrifices were made and rituals performed to discover the 'will of the gods' or to try to influence human
affairs. This idea still prevails, and many people all over the world use lucky charms, engage in superstitious practices, use horoscopes, and still have some kind of belief that there are such ways of influencing their lives. The gods may be dead, but 'Lady Luck' still survives.
The astragalus is a small bone, about an inch cube, found in the heel of hoofed mammals. Astragali have six sides but are not symmetrical, so there is no way of knowing which way they will eventually come to rest. For many ancient civilizations, astragali were used by priests to discover the opinions of their gods. It was customary in divination rites to roll, or cast, five astragali. Typically,
each possible configuration was associated with the name of a god and carried with it the sought-after advice.
Image
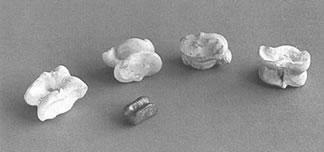

Astragali from the heel of a sheep showing the four positions of rest.
The small one in the foreground is made from pottery
Image


The game of Hounds and Jackals dating from 1800 BCE found in an Egyptian tomb
The astragali have been used from classical times for gambling, and similar stones are still in use today for games like 'fivestones' or 'jacks'.

Die A
Gradually, over thousands of years, astragali were replace by dice [see note 1 below], and pottery dice have been found in Egyptian tombs. The earliest die known was made from pottery and excavated in Northern Iraq dating from about 3,000 BCE. It has dots arranged as in (Die A).

Die B
Die (B), from about 1400 BCE found in a tomb in Egypt, shows consecutive numbers opposite each other.

Die C
Dice with other markings like the names or portraits of gods have been found, probably used for special games or rituals, and others where some numbers are repeated, or 'loaded', for special purposes or possibly for cheating (Die C).
Once the Greeks had worked out the geometry of the polyhedra, dice of other shapes began to be constructed. However, whether cube or polyhedral, the shapes were not entirely regular and were therefore biased.
Over time, gamblers would get used to using the same dice, and have an intuitive idea of how they would fall, but given another set of dice, the odds would be different. Later, as the manufacture of dice became more exact, some ideas of the possible combinations of number began to emerge.
The Earth and The Cosmos
There were many other forms of rituals hoping to overcome the randomness of nature and man's condition. A few of these which became of particular mathematical interest are geomancy, the nine square grid or magic square, and temple designs, the ancestors of board games.
Geomancy
Geomancy means divination of or by the earth , and is a system of 16 mathematically related arrangements of stones, beans or other available small objects used to make decisions, answer questions, or foretell the future. The stones are cast upon the ground and the pattern formed is interpreted. The symbols represent a series of binary 'opposites' like good and evil, male or female, sadness and happiness, etc. Combinations of these opposites can be used to represent odd and even numbers.
Image
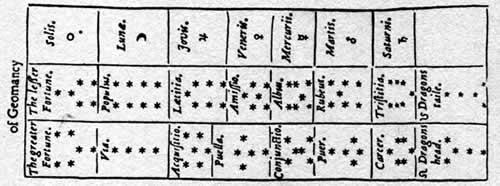

The sixteen figures of the Geomancy system of Divination. The headings of the columns are: "The greater fortune" and "The lesser fortune". From a Book of Occult Philosophy published 1655. Notice that each pair of shapes are associated with the traditional signs for the planets and that each configuration could be interpreted from the throws of two dice.
The Grid of Nine Squares
The Nine square grid is said to come from an ancient system for the division of land, probably from feudal India. In China the nine-square configuration was supposed to be an ideal arrangement, with eight farmers' fields surrounding a central well. The grid of nine squares, or a circle divided into nine sections by straight lines often appears as a central form in Tibetan sacred diagrams. In
Scotland, the pattern was used at Beltane (the eve of May) where eight squares were cut out from the turf, and a bonfire lit on the central square.
In this way, from practical beginnings in different cultures, the nine-square grid acquired mystic importance and symbolised divine order, and the representation of control by the gods.
Magic Squares are directly related to the Sacred Grid, supposedly being the numerical mystery which underlies their physical form. The simplest magic square is the square of nine, ascribed to Saturn, where each row and column adds up to 15; the total of the rows and the columns is 45, and the diagonals 30. The 4x4 square with row and column numbers 34 is
assigned to Jupiter, the 5x5 with row or column numbers 65 to Mars, and so on for the Sun, Venus, Mercury and the 9x9 square with row or column numbers 369, to the Moon [an NRICH article on Magic Squares can be found here at nrich.maths.org/1337].
As with other devices, these magic squares are all said to have correspondences to different numbers, various deities, days of the week, natural objects, different qualities, and so on. In the Hindu Temple Yantra [see note 2 below] you can see the nine squares, the 'sacred space', or source of energy, in the centre.
Image
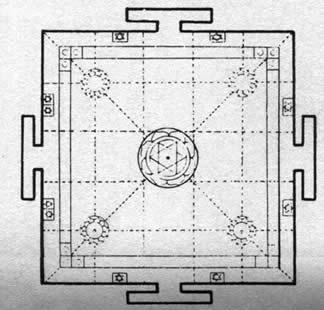

This is a Yantra from a Hindu Temple. Yantras (or Mandalas) are used as a focus for mystical contemplation and often for the basis of design for a temple. This one is based on a 5 x 5 square, with the 'sacred space' of the 3 x 3 square in the centre.
Board Games are clearly linked with divination, astrology and sacred geometry, and the designs of the boards can show their sacred or occult origins. The popular game of 'snakes and ladders' is controlled by the throw of dice, and the ladders and snakes originally referring to good and bad fortune, now refer to good and bad 'luck' in the progress of the game. In some cases the designs of the boards are the same as the plans of temples and holy cities with a 'sacred space' in the centre.

This is the board for the ancient Korean game of 'Yut' or 'Nyout' The board can be made of cloth or paper, or can be drawn on the floor. It is played with four 'Yut Sticks' of semi-circular section, and the way they fall determines the move of a token. The shape can be square or circular and represents the division of the world into twenty outer regions and nine central spaces.
The game of 'Nine Men's Morris' is played with counters on the dots on this board. The design is said to represent the four elements, (earth, air, fire and water) the four winds, or the four cardinal points of the compass, and the central sacred area was a symbol of rebirth or renewal.

The game was supposed to have originated in Egypt, and was known to the Romans. This is a picture from the 13th century of the game being played in England.
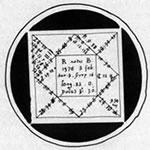
This is a traditional diagram used for the Horoscope of Robert Burton from his tomb in Christchurch in Oxford. This clearly has a link with the diagrams from sacred architecture and board games.
Mathematics and Magic
In ancient times, few people could understand even the simplest arithmetic and geometry, and the confusion of mathematics with magic has a long history.
People who had knowledge of the regular movements of the heavens were able to predict the position of planets, and the particular the times when astronomical events appeared in certain sections of the sky. In ancient civilisations these were highly skilled technicians, called 'priests', and their activities were partly scientific, and partly religious. In Europe, after the arrival of
Christianity, the religious aspect of these practices was condemned as superstition. Because numbers were used in these processes, anyone who used numbers was regarded with considerable suspicion. In this way genuine mathematicians were looked upon with suspicion by the ignorant, and the titles of Astrologer, Mathematician and Conjurer were virtually synonymous.
An early Bishop of the Church, St. Augustine of Hippo (354-430 CE) once said:
"The good Christian should beware of mathematicians and all those who make empty prophecies. The danger already exists that mathematicians have made a covenant with the devil to darken the spirit and confine man in the bonds of Hell."
Augustine was arguing that belief in astrology denies the freedom of the will.

Roger Bacon (1214 - 1292), often called England's first Scientist, had a reputation as a 'great necromancer' because of his ingenious experiments and John Dee (1527 - 1609) probably one of the foremost mathematicians in Europe of his time, gained a reputation as a 'Conjuror' while he was at Oxford because he was respnsible for developing a simple mechanical device by which an actor appeared to fly, and people claimed he was in league with the devil. [see note 3 below]
John Dee


Image


Following the foundation of the Oxford chairs in mathematics and astronomy in 1619, some parents kept their sons away from the university in fear of them becoming contaminated by the 'Black Art'.
As the predictive power of astronomy and other practical uses of mathematics became apparent, mathematicians were able to dispel the idea that many events were not controlled by the goddess Fortuna, but could be explained in a rational way.
This is the title page of Robert Recorde's The Castle of Knowledge published in 1556. It is his fourth book for the self-education of craftsmen and artisans and shows how to make the instruments for astronomy and navigation. The blind goddess Fortuna stands on the unstable sphere holding the wheel of chance, while the Spirit of Knowledge stands on a stable cube holding the navigator's dividers and the sphere of destiny.
The Beginnings of Probability
Since dice were used in gambling, in religious ceremonies and for divination, it is believed that those who used the dice had a good intuitive idea of the likely frequency of various number combinations. The first printed document showing the possibilities with three dice was the Latin poem De Vetula , which shows all the combinations for the fall of three dice, and is believed to have been written in the early 13th century. The idea of using binomial coefficients to calculate the possibilities appears in the poem, but is not taken up until much later [see note 4 below].
Image


Part of the poem De Vetula written in the 13th century, shows the different combinations of three dice. Notice the written numerals on the left of the text.The written numerals for the number combinations appear to the left of the poem.
Image


(1501- 1576)
Girolamo Cardano
Since the Christian Church was against gaming, and there was much superstition about divination, it is not surprising that a theory of probability did not begin to appear until the 16th century. Cardano, writing with considerable personal knowledge of gambling, recognised that if the die was honest, each face would have an equal chance of appearing. His manuscript, Liber De Ludo Aleae , was written about 1526 but only found after his death, and not published until 1663. He gave tables of the results for one, two and three dice, but these are not all correct. However, Cardano is credited with recognising that the abstraction of the 'honest die' is the key to a theory of probability based on mathematical principles.

Nicolo Tartaglia (1500-1557)Tartaglia (1500 - 1557) and others discuss various versions of the division of the stakes when a gambling game is stopped, called the 'problem of points', and this shows that Cardano's ideas were likely to be common knowledge among scholars of the later 16th and early 17th century.
Galileo (1564 - 1642) wrote on probability but his work was not published until1718. He stated that with three dice there can only be one way of obtaining a 3 (1,1,1) and an 18 (6,6,6) but there are three combinations for obtaining a 6 (4,2,1), (3,2,1) and (2,2,2) which can occur in different orders making 10 possibilites and four combinations for a 7 (5,1,1), (4,2,1), (3,3,1) and (3,2,2) which lead to fifteen possibilities. However, although 9 and 12 could be made up in the same number of ways as 10 and 11, from their experience, gamblers claimed that the occurrence of 10 and 11 were more likely! Galileo showed that the total number of possible throws with three dice are 216, and he gave a table of the number of possible throws for a total of 10, 9, 8, 7, 6, 5, 4 and 3, showing that the throws for 11 to 18 were symmetrical with these. In this way he showed that there were 27 possible throws to obtain a 10, and 25 for a 9.
Image


This is a copy of the table Galileo published in his Sopra le Scoperte de I Dadi (Concerning an Investigation on Dice). Here he shows clearly how to count the different combinations of the various throws.
Pascal's Triangle
By the mid 16th century the theory of probability became established on a rigorous basis with the work of Pascal and Fermat. However, as we have seen, the idea of the application of 'Pascal's Triangle' had been suggested as early as the 13th century but forgotten for some 200 years. The triangle itself was known and published before, by Stifel (Arithmetica Integra 1543) Tartaglia (Trattato 1556) Stevin (Arithmetic 1625) Pierre Herigone (Cours Mathematique 1634), and we also know it was known to the Chinese and the Arabs by the mid 13th century, but Pascal was the first to apply it to probability.
For pedagogical notes:
Use the notes tab at the top of this article or click here .
Notes
- The word 'die' (plural 'dice') come from the Latin verb 'dare' (pron. da-ray) to give its participle dadus means 'given by the gods'.
- The word Yantra is a Sanscrit word meaning a mystical diagram or picture. They contain geometric items and archetypal shapes and patterns of squares, triangles, circles and other floral patterns. In contrast, a Mantra is a spoken verse or poem.
- At this time, 'Mathematics' included the applied mathematics of physics, statics, mechanics, hydraulics, and other practical arts. This is clear from John Dee's famous 'Preface' to the 1570 English Edition of Euclid.
- It is possible that the scholar who wrote this poem might have been aware of the 'number triangle' of the Arabs.
References
General Background and History
Some Books for the Classroom
Jenkins, G.W. & Slack J.L. (1979) Classroom Experiments with Dice . St Albans. Tarquin Publications
Woods, G. Symmetry Dice . St Albans. Tarquin Publications
Benson, S. (2005) Ways to think about Mathematics:Activities and Investigations for Grade 6 . California. Corwin Press. This is a useful book with many examples of activities. There are sections about probability and binomial coefficients.
Weblinks
Here is a shop for all kinds of dice : large; small; all colours; with numbers; with spots; blank; arithmetic symbols; money symbols; polyhedral; round (yes round!); loaded; and for cheating! http://www.dice.co.uk/index.htm
