Circle packing
Equal circles can be arranged so that each circle touches four or
six others. What percentage of the plane is covered by circles in
each packing pattern? ...
Problem
Equal circles can be arranged in regular square or hexagonal packings to fill space as shown in the diagram so that each circle touches four or six others.
Image
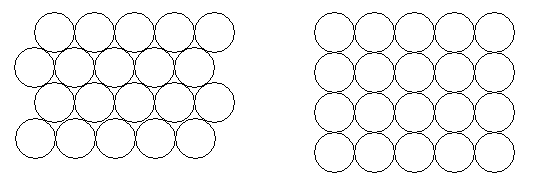
What percentage of the plane is covered by circles in each packing pattern? How is this of use in packing cylindrical cans and what are the advantages and disadvantages of the two packing systems?
Click here for a poster of this problem.
Student Solutions
James of Christ Church Cathedral School, Oxford and Alexander from Shevah-Mofet School, Israel sent very good solutions to this question.
To find the percentage of the plane covered by the circles in each of the packings we must find, within the original pattern, a shape that tessellates the plane and in each case this can be done in different ways. In one case it could be a tessellation of squares, either surrounding the circles or formed by joining the centres of the circles. In either case the calculation of areas is the same.
Image
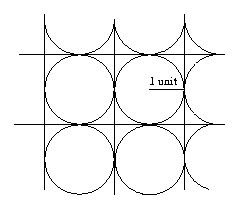
Image
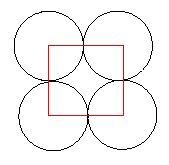
Let us say that the radius of the circle is $1$ unit. The area of the circle is $\pi$ and the area of the square is $4$ square units. Therefore the proportion of the plane covered by the circles is $\pi/4 = 0.785398\ldots = 78.5\%$ to 3 significant figures.
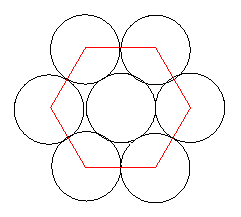
In the other case the packing of the plane can be produced by a tessellation of hexagons (like a honeycomb).
Image
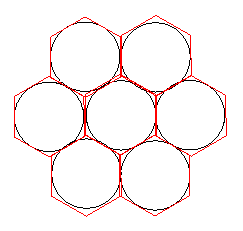
The hexagon touches the circle at the midpoints of its sides, the distance between the midpoints of opposite sides is $2$ units, the lengths of the sides of the hexagon are $1/\sqrt{3}$ . The area of the hexagon can be found by splitting it into six equilateral triangles and the total area is $6\times (1/\sqrt{3}) \times 1 = 2\sqrt{3}$ square units.
To get the proportion of the plane covered by the circles we must divide by $pi$ by $2\sqrt{3}$ to get $0.90689\ldots$ or $90.7\%$ to 3 significant figures.
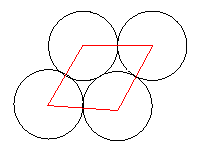
This packing can also be done with a tessellation of rhombuses which have angles of $60$ degrees and $120$ degrees. It can be shown that the area of the rhombus is $2\sqrt{3}$.
Image
Here is another method for Circle Packaging from Suzanne and Nisha of the Mount School, York:
Image
Image
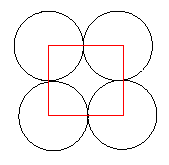
We worked out the percentage of each plane covered by circles, by dividing the two patterns into hexagons and squares (see the diagrams above) We worked out the percentage of each hexagon covered by circles and the percentage of squares covered by circles.
Hexagons
A hexagon is 6 triangles area of 1 triangle: base = 2cm ; height = 1.73cm so area of 1 triangle = 1.73cm2 and the area of the hexagon is 10.38cm2.
There are 3 whole circles in each hexagon. radius of circle = 1cm so area = $\pi$ cm2 and area of 3 circles = 3$\pi$ cm2
% of hexagon covered by circles = (3$\pi$/10.38) x 100 = 90.8% (rounded) Notice how not using exact values for the height of the triangles in the hexagon calculation means this is 0.1 cm2 off - a type of rounding error introduced by rounding off numbers before the answer.
Squares
Each square has area = 4cm2
In each square, there is 1 whole circle
area of circle = $\pi$
% of square covered by circles = ($\pi$/4) x 100 = 78.5% (rounded) This means that you could fit more cylindrical cans in a container using the `hexagon' pattern. Advantage of the `square' pattern is that you could maybe fit things in the gaps, which are larger than in the hexagon pattern.
