Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Shapes in the Alphabet
Age 5 to 7
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Shapes in the Alphabet
We are going to look at capital letters, not for writing or spelling, but as shapes with various different properties.
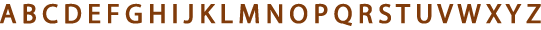
Some letters have horizontal lines, some have vertical lines and some have both. Some letters enclose a space and others do not. Some can be drawn without taking your pencil off the paper or going over the same line more than once, others can't.
In this challenge we are going to find sets of letters that go together because they share some features.
Here are some letter shapes that go together in a set -
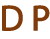
What properties do they share? What other letters could go with them?
Scroll down to find some more letters in the set.

Here you are:

Were you right or do you think differently now?
Scroll down to find some more letters in the set.

Here you are.

Can you find other letters that share properties with these letters? There are ten of them.
Now we are going to try with a different set of letters. Here are two of them.

Scroll down to find some more letters in the set.

Here you are.

Were you right or do you think differently now?
Can you find other letters that go with these? There are nine of them.
Now you can make your own sets of letters. Try challenging a friend in the same way with your sets of letters.
Why do this problem?
This problem uses a familar resource, the capital letters of the alphabet, in an unusual way. This enables learners to work with interesting shapes which are non-threatening and easy to talk about. The problem encourages children to make hypotheses and give reasons for their suggestions, then alter their
hypothesis based on new information.
Possible approach
Before starting this activity, it would be good to talk with the group about the shapes of different capital letters. Perhaps one child could describe a particular letter for their partner to guess which one it is. In this way, the class will begin to develop a shared language which might include words such as lines, straight, curved, horizontal, vertical. Learners might need help describing
the enclosed area that some shapes make.
The two challenges could be displayed on the interactive whiteboard (or screen), so that to start with, each pair makes a hypothesis based on the first two letters. These initial ideas could be shared, focusing on reasons for them. Of course at this stage, a number of conclusions could be drawn. As you scroll down to the next part, ask pupils to consider altering their hypotheses and
continue in this way. Again, it is the reasons for changing their minds (or not!) that are useful to emphasise. This sheet of letter shapes could be photocopied for class use or alternatively, learners could work in pairs at a computer.
Key questions
What is the same about these two letters?
What is the same about the letters in this set now?
Which other letters could go with them?
Possible extension
Children could make their own versions of this problem by finding other sets of letters that go together and then challenging a friend to find the set when a few are given at a time.
Possible support
It might help some learners to have each letter on a separate piece of paper or card so that they could be physically moved around and therefore compared more easily with each other.