LCM Sudoku

Each column, each row and each 3x3 box must have the numbers 1 to 9.

No column, row or box can contain the same number more than once.

The nine letters in the grid each represent a different number from 1 to 9.

The numbers at the end of the rows and at the bottom of the columns are the Lowest Common Multiples (LCM) of the letters in that row

The LCM of the variables b, w, m and c in the fourth row is 504.

As an example, the LCM of 8, 9, 6, 4, 2, 5 and 7 is 2520.

Here is a grid for you to print out and work on.

Alison worked out the value of the letters in the following order: w, a, b, m, c, v, e, n, d

Here is the complete route she took through the lettered cells:

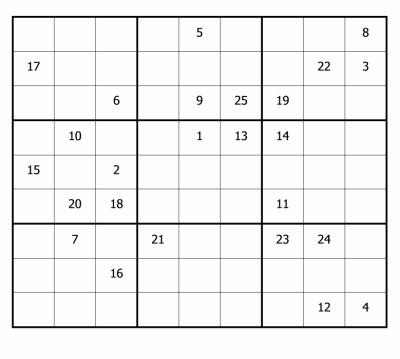
Charlie worked out the value of the letters in the following order: a, m, b, w, c, v, e, n, d

Here is the complete route he took through the lettered cells:

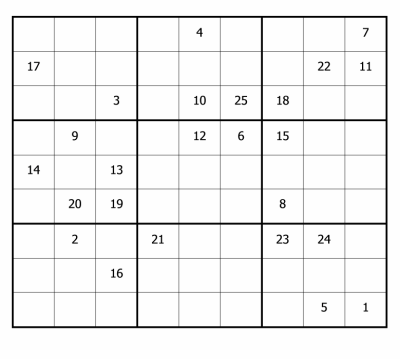
Steve worked out the value of the letters in the following order: c, v, w, a, b, m, e, n, d

Here is the complete route he took through the lettered cells:

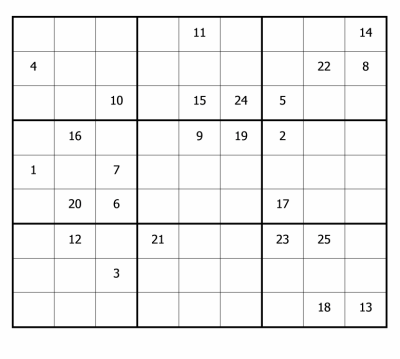
Can you work out the values of the nine letters in the same order that they did?

Can you work out the values of the letters in any other orders?

If you'd like to discuss this problem and your strategies for solving it, visit the blog

After finding the values of all the variables, you can solve the rest of the Sudoku using standard techniques and strategies.

Thank you to Henry Kwok for devising this Sudoku.

Published November 2011,December 2011,March 2008,April 2008.