Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Least of All
Age 16 to 18
Challenge Level 





A point $X$ moves on the line segment $PQ$ of length $2a$ where $XP=a+x$, $XQ=a-x$ and $-a\leq x \leq a$, as in the following diagram: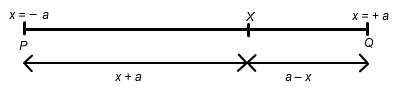
You are interested in finding the minimum value of the function $f(x)=(1 + XP^2)(1 + XQ^2)$. Without writing anything down can you suggest where the location of X that gives the minimum value(s) of $f(x)$ will be? Do you think that this will depend on the value of $a$? Once you have considered the matter, write your thoughts down as a clear, precise conjecture.
Check your conjecture using calculus to find the minimum values. Was this as expected?
Given your insights, can you suggest possible locations for the minimum values of $g(x) = (1+ XP^4)(1+XQ^4)$?
NOTES AND BACKGROUND
Conjectures are speculations which people try to prove or disprove. Some mathematical conjectures are so difficult to prove that many mathematicians, over a hundred years or more, have tried and failed to prove them. There is prize money and worldwide fame for anyone who can prove one of these famous conjectures such as The Reimann Conjecture. This is also called the Reimann Hypothesis which leads to the question "Is a conjecture the same as a hypothesis?"
The answer is, strictly speaking, no. The word hypothesis is used in pure mathematics to mean one of the conditions in a theorem, for example 'If a triangle is right-angled" is a hypothesis in Pythagoras' Theorem. A very different meaning for the word hypothesis , which is used in statistics, is a speculation which is reinforced or refuted by the acquisition of new information. Such hypotheses are not proved logically true or false but merely considered, in the light of evidence, to be more likely or unlikely to be true.
Conjectures are speculations which people try to prove or disprove. Some mathematical conjectures are so difficult to prove that many mathematicians, over a hundred years or more, have tried and failed to prove them. There is prize money and worldwide fame for anyone who can prove one of these famous conjectures such as The Reimann Conjecture. This is also called the Reimann Hypothesis which leads to the question "Is a conjecture the same as a hypothesis?"
The answer is, strictly speaking, no. The word hypothesis is used in pure mathematics to mean one of the conditions in a theorem, for example 'If a triangle is right-angled" is a hypothesis in Pythagoras' Theorem. A very different meaning for the word hypothesis , which is used in statistics, is a speculation which is reinforced or refuted by the acquisition of new information. Such hypotheses are not proved logically true or false but merely considered, in the light of evidence, to be more likely or unlikely to be true.