Andrew from Quarry Bay School sent us an image to show which numbers had come from each spinner:

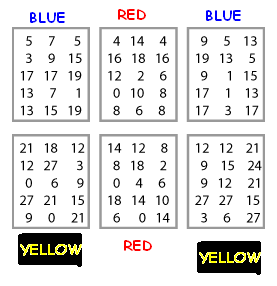
Jake from Seaford Primary described how he tackled this problem:

First I wrote down all the numbers from the red list starting with the smallest. All the numbers were in the $2$ times table so I wrote the list again with the missing numbers in.
Then I did the same with the blue and yellow list.
I looked at the other six lists. Some had only $2$ times tables so I said they were from the red spinner. Some had only $3$ times tables so I said they were from the yellow spinner. Some had only odd numbers so I said they were from the blue spinner.

Ellie did a similar thing:

First of all I wrote down all the numbers you knew were on the red, yellow and blue spinners, as in the tables.
I then checked these over with the tables with no matching colours and saw which ones fitted each.
I filled in the missing numbers which were not in the first three tables and came up with $10$ numbers for each colour and titles as well.

RED - even numbers from $0$ to $18$
BLUE - odd numbers from $1$ to $19$
YELLOW - multiples of three from $0$ up to $27$

Well done also to Jonathan from New Ford Primary, children from Stourport Primary and pupils from Dr Challenor's Grammar School who all sent very clear explanations of the ways they solved this problem.