Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
A Day with Grandpa
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
A Day with Grandpa
William went to spend the day with Grandpa. Grandpa was busy measuring a rug to put on the hall floor. He was using yards, feet and inches to measure with. Grandpa always did.
William was learning about area at school. "I wonder what the area is?" he pondered.
Grandpa wrote down his measurements and drew this sketch.
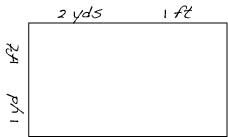
"It's two yards and one foot by one yard and one foot. There's three feet in a yard, so that's seven foot by four foot. Let me see, that's twenty-eight square feet and that's .... hmm ..... three square yards and one square foot."
Was his calculation correct?
"Let's measure the doormat," he said, "You do it." William used Grandpa's measuring tape.
"The doormat's two feet and six inches by one foot three inches," he announced.
Grandpa did another sketch.

He thought for a while.
"There's twelve inches in a foot, so it's three square feet and eighteen square inches," he announced at last.
Was this calculation correct?
Grandpa was getting into his stride. "Let's measure the rug in front of the fire, too," he said excitedly.
It was two yards, one foot and five inches long and one yard, two feet and seven inches wide.
"How do you work it out?" inquired William. "You multiply them together, of course," said Grandpa airily.
He wrote some figures on his paper.
"Wow! How do you do that?" asked William peering at it.
Grandpa looked at his paper for a long time.
"I can't remember," he hesitated, "Can you think of a way to do it?"
Can you think of a way to do it?
Why do this problem?
This problem challenges children's understanding of the concept of area rather than simply requiring them to follow a rule for finding areas of rectangles. These calculations should also help learners to see the advantages of the metric system as well as understand it more fully!
Possible approach
As an introduction to this problem, invite children to tell you about different words they have heard used in the context of measuring distance. (This might reveal some interesting misconceptions.) Focus on those that are units of measurement and ask the learners to suggest when each might be used. You could group the words on the board to show those that are metric units and those that are
imperial, which would lead into a discussion of which are most common nowadays.
Go onto look at the problem itself, perhaps by telling the story orally and drawing Grandpa's sketch yourself on the board. Ask children to talk in pairs about how they would check the calculation, and then discuss it as a whole class. You might find that some pairs would like to annotate your drawing which would be helpful! Set the children off on the other parts of the question in pairs or
small groups, making sure there is paper available should they want it.
In a plenary, take the opportunity to share different ways of working on the solutions which show good understanding of the concept of area and the use of square units. Which system of units do the children think is easiest to work with?
Key questions
Have you drawn a diagram or sketch?
Can you find any complete square yards or complete square feet?
Possible extension
Children may enjoy measuring some objects in the classroom and using both metric and imperial measures to work out their areas.
Possible support
Drawing a diagram of the two sketches on squared paper might help when it comes to dividing them up into complete square yards and square feet.