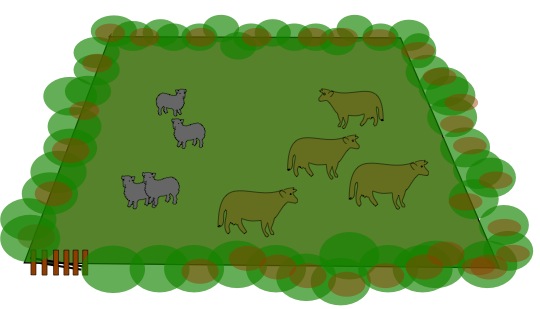
In this field we could say, because of the number of animals there, that each cow can see 4 sheep and 3 (other) cows. This could be worded as follows "Each cow can see one more sheep than cows." There are obviously 4 sheep and 4 cows in the field as you see it.
But here are some questions about different fields in which you have to find out how many sheep and cows there are in each field.

In field number 1, each cow can see twice as many sheep as cows; each sheep can see the same number of sheep as cows, so how many cows and sheep are there?

In field number 2, each cow can see three times as many sheep as cows; each sheep can see the same number of sheep as cows, so how many cows and sheep are there?

In field number 3, each cow can see twice as many sheep as cows; each sheep can see one more sheep than cows, so how many cows and sheep are there?

In field number 4, each cow can see twice as many sheep as cows; each sheep can see two more sheep than cows, so how many cows and sheep are there?

In field number 5, each cow can see three times as many sheep as cows; each sheep can see twice as many sheep as cows, so how many cows and sheep are there?