 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Same Height



- Problem
- Student Solutions
A trapezium is divided into four triangles by its diagonals. Suppose the two triangles containing the parallel sides have areas a and b , what is the area of the trapezium?
The following solution was done by Ling Xiang Ning, Allan from Tao Nan School, Singapore
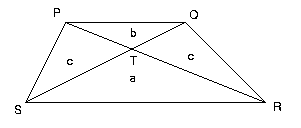
First note that triangles SPR and SQR are equal in area (same base and height) so triangles SPT and RQT are equal in area; suppose this area is c .
Now triangles SPT and TPQ have the same height (with their common base on SQ) and the ratio of their areas is:
$$ \frac{c}{b} = \frac{\text{Area}(SPT)}{\text{Area}(TPQ)} = \frac{ST}{TQ} $$
$$ \frac{a}{c} = \frac{\text{Area}(SRT)}{\text{Area}(TRQ)} = \frac{ST}{TQ} $$
hence $ c/b = a/c $.
Then $ c^2 = ab$ and $c = \sqrt{ab}$
Therefore, the total area of the trapezium is $ a + b + 2\sqrt{ab}$.