 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Not a Polite Question



- Problem
- Solutions
If her age is 10 t + u (where t is the tens digit and u is the units digit) then reversing the digits gives 10 u + t. and the sum is 11 t + 11 u, which is a multiple of 11. We know this has to be a square number. Ong Xing Cong from Singapore sent in the following solution.
11 t + 11 u = 11 x 11 = 121
t + u = 11
65 - 56 = 3 x 3
She is 65 years old.
The best solutions do not need trial and improvement methods and
they show that the answer or answers found are the only possible
answers. Knowing the digits add up to 11 ( t + u
= 11), you can also use (10 t + u ) - (10
u + t ) = 9 t - 9 u = 9(
t - u ) As this is also a square number you know
( t - u ) is either 1, 4, or 9. The solutions for
4 and 9 don't give whole number values for t in 0
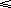 t
t
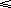 9.
9.