 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Arrowhead



- Problem
- Student Solutions
Like Quad in Quad (June 1998) the key to this problem is using the fact that, when the midpoints of the sides of a triangle are joined, the join is parallel to the third side and half the length of the third side.
This solution came from Murat from Turkey.
Due to the Thales relationship, SP and QR are both parallel to BD, thus to each other. Moreover they are half as long as BD. A similar relationship holds among PQ, RS and AC. Therefore PQRS is a parallelogram.
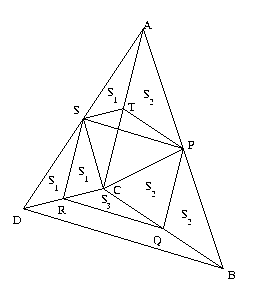
Let T be the midpoint of AC.
In the above figure, the areas of the triangles marked by the same symbol are obviously equal (look for triangles on equal bases which have the same height). Moreover Area (CST) = S 1 , Area (CPT)= S 2 and Area (TPS)= S 3 . The following equations are obviously true:
| Area (ABCD) = | 4( S 1 + S 2 ) |
| Area (PQRS) = | ( S 1 + S 2 + S 3 ) + ( S 1 + S 2 - S 3 ) |
| = |
2( S 1 + S 2 ) =
$\frac {1}{2}$ Area
(ABCD)
|