Copyright © University of Cambridge. All rights reserved.
'Consecutive Negative Numbers' printed from https://nrich.maths.org/
Show menu
Consecutive Negative Numbers printable worksheet
Do you notice anything about the solutions when you add and/or subtract consecutive negative numbers?
Take, for example, four consecutive negative numbers, say $$-7, -6, -5, -4$$ Now place $+$ and/or $-$ signs between them.
e.g.
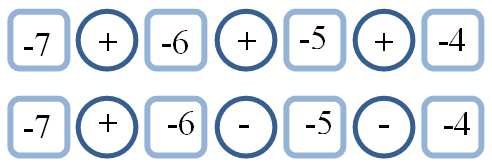
There are many more possibilities. Try to list all of them.
Now work out the solutions to the various calculations.
e.g.
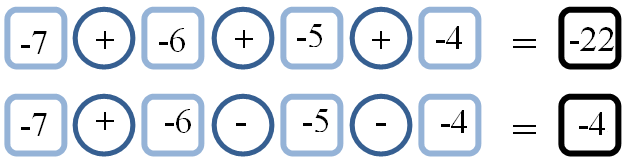
Choose a different set of four consecutive negative numbers and repeat the process.
Take a look at both sets of solutions. Notice anything?
Can you explain any similarities?
Can you predict some of the solutions you will get when you start with a different set of four consecutive negative numbers?
Test out any conjectures you may have.
Can you explain and justify your findings?