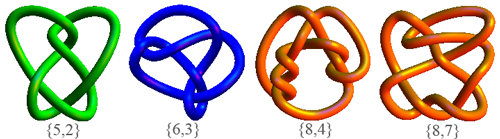If you make a knot from plastic pipe you could imagine filling the pipe with a fluid such as water. The fluid would then be able to flow around the pipe in some direction. In the video we've tied a pipe into a trefoil knot and stencilled some arrows on its surface so you can see the direction of flow.



Notice that the trefoil knot can be deformed - in this case simply by turning the whole knot around - into an exact copy of itself except that the direction of fluid flow has been reversed. If you can do this to a knot, then the knot is invertible .

This figure of eight knot is also invertible. Can you see why?


Most small knots are invertible. In this table of small knots with up to 8 crossings only one is listed as not invertible. We're not sure about the knot listed there as {8,10} - you might be able to help us decide on that one!

You can use the symmetry of many of the drawings to convince yourself that the knots are invertible, but sometimes the drawing doesn't help and you'll have to get a piece of string and make the knot for yourself before you can see it.

Here are some of the more interesting cases to try. Be careful, the first one is trickier than it looks!