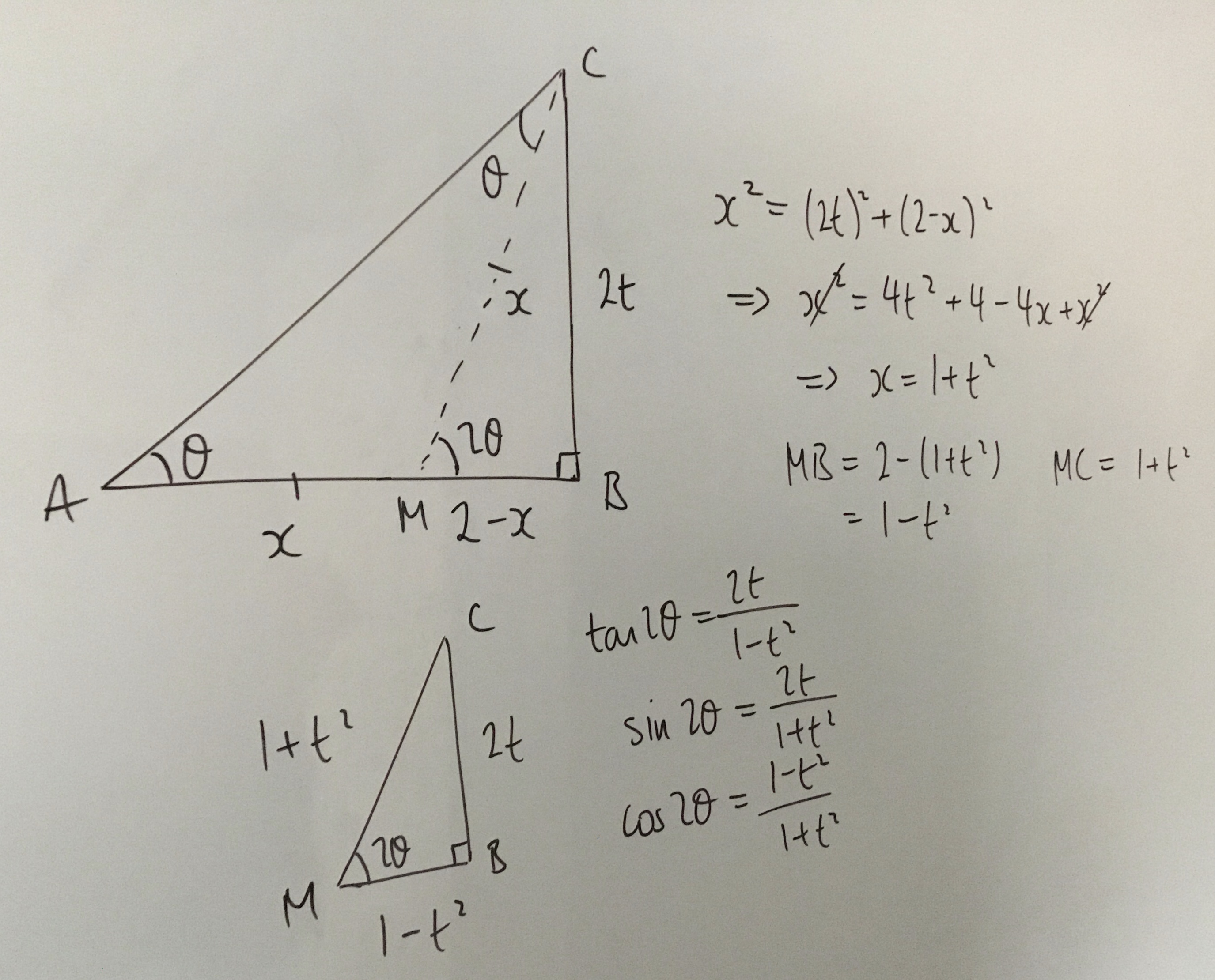Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
T for Tan



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done to Dylan from Brooke Weston, Joshua from Bohunt Sxth Form, Mykhailo and Daniel, Ilan, Adam and Alexander from JFS, Soumya from King's Maths School, Josh from Queen Elizabeths Grammar School Alford, Bertie from Sir William Borlase's Grammar School, Isy and Rafi, all in the UK, and to DongYeon, who all used Pythagoras' Theorem first to solve the problem. Here is Dylan's work:
Three mathematicians from Simon Balle All-through School wrote a two-page paper explaining their work. They used a slightly different method. You can download their paper here.
DongYeon suggested generalising the problem:
This will work for any right triangle of any length. Let's use a variable $L$ instead of $2.$
$h = L\tan \theta$
$(Lt)^2 + (L - x)^2 = x^2$
$x = \dfrac{L(1 + t^2)}2$
$L - x = \dfrac{L(1 - t^2)}2$
$\tan{2\theta} = \dfrac h{(L - x)} = \dfrac{Lt}{\frac{L(1 - t^2)}{2}} = \dfrac{2t}{1 - t^2}$
$\sin{2\theta} = \frac hx = \dfrac{Lt}{\frac{L(1 + t^2)}{2}} = \dfrac{2t}{1 + t^2}$
$\cos{2\theta} = \dfrac{L - x}x = \dfrac{\frac{L(1 - t^2)}2}{\frac{L(1 + t^2)}{2}} = \dfrac{1 - t^2}{1 + t^2}$
Note that this is not necessary: using $2$ rather than $L$ did not mean that $\tan{2\theta}=\dfrac{2t}{1 - t^2}$ is only true for triangles where one side is less than $2$. It is true for all acute values of the angle $\theta .$ So in this case, you can prove the formula using a side of length $L,$ or of any other length. When this is the case, it is often most efficient to choose a simple number, like $1$ or $2.$
You may also like
Shape and Territory
If for any triangle ABC tan(A - B) + tan(B - C) + tan(C - A) = 0 what can you say about the triangle?
Why Stop at Three by One
Beautiful mathematics. Two 18 year old students gave eight different proofs of one result then generalised it from the 3 by 1 case to the n by 1 case and proved the general result.
Reflect Again
Follow hints to investigate the matrix which gives a reflection of the plane in the line y=tanx. Show that the combination of two reflections in intersecting lines is a rotation.