Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Train Routes
Age 5 to 7
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Train Routes
Here we have a train line that has different routes from Appleby to each of the main stations of Barkton, Cheston and Dorby, because there are two crossing-over lines passing through Barkton and Cheston.
The smaller stations at Yanbridge, Zogborough, Worsby, Xanly, Underton and Vilham just have a single track running through them:
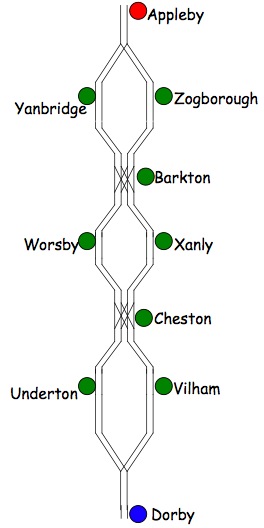
What are the different routes that you can have to end at Cheston?
What are the different routes that you can have to end at Dorby?
You might like to then invent your own routes that may go further than this one and then answer similar questions that you can think up.One of the main reasons for this challenge is to find ways of approaching such a problem. When introducing it to the class, it would be good to put the problem into a context, perhaps by talking first about local journeys. You could ask the children if they have ever seen maps of train/bus/tram/underground routes drawn in stations or on the walls of the vehicles themselves. It would be good to discuss how the maps are "models" for the routes taken - they are simply a way to put the routes on paper to make it easy to understand.
You could then show your pupils the route in the problem and ask a few questions about it so that you are sure they understand the way it is drawn. For example, if I came from Appleby, what station would the train stop at after Barkton? (This could be Worsby or Xanly.) You might like to begin the first part of the problem as a whole class, asking them how they will know when they have all the different routes. How will they record the routes that they find? This is a good opportunity to model having a system. Your class might suggest several routes from Appleby to Cheston, and you could pair them up so that the two which both visit Yanbridge, for example, are together. In this way, even if this time they have not found them systematically in the first place, the children can see how they can develop a system next time.
Children might like to try the investigation Simple Train Journeys after having a go at this problem, which uses similar ideas but in a more open context.