Copyright © University of Cambridge. All rights reserved.

'What's Inside/outside/under the Box?' printed from http://nrich.maths.org/

Show menu


Shape and space offers wonderful opportunities for enriching children's experiences in mathematics in practical ways, as well as making links with other areas of the curriculum, such as art, religious education and history. If it is simply reduced to making tables about the properties of different kinds of triangles and quadrilaterals then we are missing plenty of mathematical treats.

At Key Stage 1, some of the initial ideas are related to descriptions of position and shape, and children need to be exposed to plenty of activities that enrich their use of language. Vocabulary such as "over", "under", "below", "above", "before", "after", "inside", "outside", "round", "square", "straight", "curved", and so on, is all-important. One activity that I enjoy using with young children is attribute tables that ask children to place objects in the places that match the headings of the rows and the columns. It is important to start off with practical equipment such as Compare Bears and to encourage children to talk about the problems by working in pairs. Once children have had plenty of practical experiences with arranging concrete objects on grids, they should be ready to tackle something slightly more abstract such as:

What Shape and Colour :

Fill in the empty boxes.

That problem is based on the vocabulary describing shape and colour.
Coloured squares builds on this but adds in vocabulary about position too:

Use these clues to colour each shape:

  • Blue is between green and red
  • Orange is below green
  • Yellow is to the left of both purple and orange.
Able pupils could be encouraged to make up some problem like this. Making them up is much more difficult than doing them, and you may want to provide some coloured multilink as a support.

After becoming familiar with the basic ideas about position and description, the children will be ready to explore twodimensional shapes and their properties. This is often done by filling in the missing things in tables, but a more interesting approach is to do something practical. Plenty of the properties of shapes can be explored with groups of children and loops of string, and the conversations will give the children more opportunities to communicate their mathematical understandings to each other, as well as providing you with an insight into their understanding. A loop of string and three children to each loop can be used to explore triangles. There are plenty of questions to ask:

  • What shape can you make if everyone makes a corner?
  • Can you make one with all the sides the same length?
  • How many lines of symmetry does it have?
Isosceles and right-angled triangles can be made in the same way and children can explore their lines of symmetry, the angles in them and how many different kinds of triangle they can make. Recordings of the findings can be made using drawings or sticking down the string on big sheets of paper and making a display for the classroom walls.

Here is a problem that extends these ideas into quadrilaterals and their properties:

Stringy Quads
You will need a loop of string for this activity and three friends to work with.
  • With all four of you holding part of the string, make a quadrilateral that has one line of symmetry.
  • How could you convince someone else watching that your shape has just one line of symmetry?
  • Now use the string to form a quadrilateral with two lines of symmetry.
  • Again, how could you prove where these two lines lie?
  • Now use the string to form a quadrilateral with three lines of symmetry.
  • Is it possible? Explain.
  • Now use the string to form a quadrilateral with four lines of symmetry.
  • Where do the four lines lie?
Ideas about symmetry can be extended by considering the symmetries of equilateral triangles. The following question starts to build up the ways in which the rotations and reflections of the triangle can be considered by looking at the number of ways the triangle could be posted into a shape sorter. On the NRICH website this problem has an interactivity with it as well, which makes it appealing for children to experiment with and also makes it ideal for whiteboard use.

Turning Triangles
  • How many different ways can you post this triangle into the black hole?
  • A dot has been drawn on the triangle to help you keep track.
  • The triangle is white on the other side.
  • If you can post the triangle with either the grey or white colour face up, how many ways can it be posted altogether?
The triangle can be posted in as it is, turned through 120 degrees, turned through 240 degrees, flipped over about a vertical line of symmetry, flipped over about a line of symmetry through the bottom left-hand corner and flipped over through a line of symmetry through the bottom righthand corner. So there are six symmetries altogether.

From this starting point a further question asks children to work out the ways in which these different turns and flips can be combined and whether they are equivalent to one another. Here is a follow-up question that starts to explore this:

Sorting Symmetries
Naomi has a triangle which is blue on one side and yellow on the other. It has a dot in one corner on each side. How many ways are there of posting this triangle through a triangular shaped slot?

All these ways of posting the triangle are different. They can be called symmetries of the triangle. Can you work out a way to describe each one? You might like to choose a symbol for each.

Naomi finds that she can turn the triangle and then flip the triangle vertically so that she gets another symmetry. What might she have done?

Here is another problem that asks children to look for squares on a Cartesian grid. Some of them are set on the slant, so this will help to address the commonly held misconception that squares have to be set with their sides parallel or perpendicular to the sides of the page. There is also some potential to practise recording coordinates and to look for patterns in the coordinates of the vertices of squares.

Ten Hidden Squares
On the graph below there are 34 marked points (six diamonds and 28 crosses). These points all mark the vertices (corners) of ten hidden squares.
  • Each of the six diamond-shaped points is a vertex shared by two squares.
  • The other 28 points are each a vertex of just one square. All of the squares share at least one vertex with another square.
All the squares are different sizes. There are no marked points on the sides of any square, only at the vertices. (There are two near misses!) Can you find the ten hidden squares?

There is an interactive mathematical game on the NRICH website called Square It which uses some similar ideas and would give children plenty of experience to challenge the "slanting" squares misconception.

Here is another slightly zany problem for older pupils, which uses coordinates that are on an isometric grid. This odd arrangement can generate some interesting discussion about coordinates and what is special about Cartesian coordinates, as well as an exploration of different kinds of triangles.

Cartesian Isometric
The graph below is a coordinate system based on 60-degree angles. It was drawn on isometric paper.


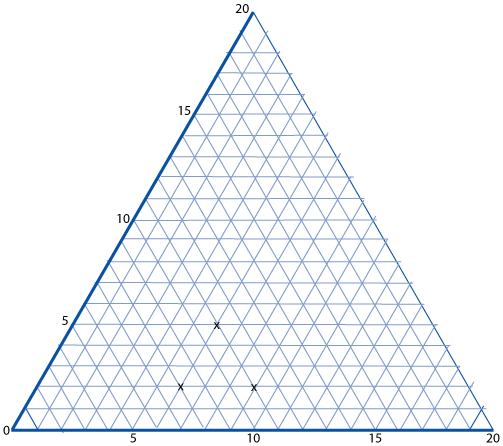
The marked points are (6, 2), (6, 5) and (9, 2). When joined they form an equilateral triangle.

The following five sets of points are also triangles.

A. (1, 13), (6, 8) and (6, 13).
B. (1, 1), (3, 3) and (7, 1).
C. (12, 1), (17, 1) and (8, 9).
D. (1, 10), (5, 2) and (6, 6).
E. (7, 5), (15, 4) and (7, 11).

What kinds of triangles are they?
Can you work out any of the angles at the vertices?

The final question will be quite a challenge for children at upper Key Stage 2 with some of the angles rather tricky to calculate. There are a few that are straightforward and can be easily worked out using the properties of isosceles, equilateral and right-angled triangles as well as the 60-degree angles in the isometric grid.

The next question would be best tackled using lots of straws or rods of different lengths. It would be best to scale the sizes up so that the rods were easy to handle, making them possibly 9cm, 12cm and 15cm long. An interactive version is available on the NRICH website.

Triangle Edges
You have lots of sticks of 3, 4,and 5 units long. How many triangles can you make using these sticks? Each side can only use one stick but a triangle can use more than one stick of the same length. A further question would be to ask "How do you know you have them all?" This leads on to the idea of proof.

So far I have only looked at problems involving shape in two-dimensional space. Three dimensions open up a whole new range of possibilities. I can remember being told by someone that geometry should be tackled with very young children in three dimensions first of all because that is our normal environment. Certainly the language of position that I referred to earlier does make a good introduction to work in three dimensions as well as two. Now let us consider a few questions that take children into three dimensions. In three dimensions practical apparatus becomes even more essential in order to help children to visualise the mathematical attributes of the shapes they are considering.

Sponge Sections
You have been given three shapes made out of sponge; a sphere, a cylinder and a cone:


  • You are going to make some shapes for printing out of these sponges.
  • How would you cut the sphere to make the largest circle for printing?
  • How could you make the largest possible circle from the cylinder? And the cone?
  • Which shape would you use to make a very small circle for printing?
  • If you cut the shapes in different ways, what other shapes for printing could you make?
  • If you make two cuts, are other shapes possible?
Using modelling dough can be quite helpful here (although you might find a bit of adjusting necessary as the dough can change shape slightly on cutting).

Instead of describing shapes in terms of their attributes, another possibility is to construct shapes from a description. Polydron, which are plastic shapes that clip together to form three-dimensional solids, are a brilliant resource for three-dimensional work.

Polydron
Can you make the solids according to the clues given?

a. This solid is a cube but:
Only three colours are needed.
One blue square touches all three red squares.
Another blue square touches only two red squares.
A yellow square touches only one blue square.

b. This solid has five pieces:
There is one square, this clips to all the pieces.
The isosceles triangles are red and green.
The edges of the red shapes do not touch red shapes.
Only red, green and blue shapes are used.

N.B. Almost any shape/solid that is constructed can be represented as a set of clues, and pupils might like to make up examples of their own to try out on their friends. What makes a good challenge? What's the smallest number of clues you can give and still make the challenge possible to solve?

Another more challenging question that really needs quite a large supply of Polydron is this one:

Triangles to Tetrahedra
What is a tetrahedron?
Here are four different triangles:



The sides of the small equilateral triangle are the same length as the short side of the isosceles triangle and the short sides of the right-angled triangle. The sides of the large equilateral triangle are the same length as the long sides of the isosceles triangle and the long side of the right-angled triangle.

You have an unlimited number of each type of triangle. How many different tetrahedra can you make? Convince us you have found them all.

I hope this has given you some more ideas to make shape and space exciting for children. Perhaps you may find that some of those children who struggle with number work surprise you when they tackle some of these geometric problems.

This article first appeared in Maths Coordinator's File issue 19, published by pfp publishing.(Although the File is no longer produced, some articles may be available through Optimus Publishing http://www.teachingexpertise.com/-821.)