Drawing Doodles and Naming Knots

'Drawing Doodles and Naming Knots' printed from https://nrich.maths.org/

Show menu

This article will introduce you to a way of naming knots - you'll need some paper and something to write with so you can try things out as you read ...

Taking a Line for a Walk

You can start thinking about knots by drawing them as lines. To draw a knot, you just need to draw a closed loop which crosses over itself, like the one in the picture. Don't worry about which string goes on top and which goes underneath for the moment.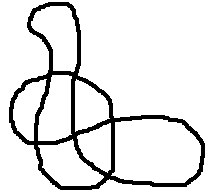

Try drawing a knot with $14$ crossings (a line which crosses itself in $14$ places).
Can you draw a knot with any number of crossings you like?

Now try adding some more information to the knot by showing which string is on top at each crossing. You can do that by drawing the knot again, but with a small gap in the "underneath" line when part of the rope goes under another part, like this:

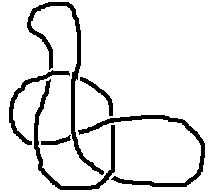
Can you choose which way the crossings go so that the string would unravel into an untangled loop?

If you draw the string so that as you follow it round it goes alternately under then over then under then over at crossings, you have drawn an alternating knot. Have a go: as you follow the string round, do you find that when you get to a crossing where you've already been, it's already the right way round? And when you get back to the beginning, does the sequence continue (if you started with an "over" do you end with an "under")?
Can you prove that this always works?

Naming Knots

Draw yourself a new knot, choosing which way the strands go at each crossing however you like.

Mark a starting point somewhere on the string and an arrow pointing in one direction or the other along the string. Now follow the string round your knot from the starting point in the direction of the arrow. The first time you come to a crossing, label it $1$. The next time you come to a crossing, label it $2$, and so on. By the time you get back to your starting point, each crossing should have $2$ labels.

What do you notice about the pairs of labels? Can you explain the observation?

Here is a knot labelled the way I have described. (The red dot and arrow are the starting point and direction).

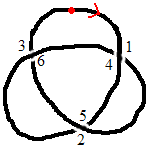
I could write the pairs of numbers for the crossings out like this:

1	3	5
4	6	2

The top line is the odd number, arranged in order. The bottom line shows which even number is at the same crossing as each odd number.

Try writing the numbers on your knot out like this.

Now see if you can draw a knot which would have these numbers: (the numbers don't tell you which strand is on top at a crossing, so you can't draw the "unders" and "overs").

1	3	5	7	9	11	13	15
12	14	10	2	4	16	8	6

In fact, we know what the top line of numbers is going to be - it's just the odd numbers $1,\ 3,\ 5\ldots$. So we could miss it out altogether. The line which is left is a kind of name for the knot.

Can you draw a knot whose "name" is $4 \; 8 \; 6 \; 2$? It might help to write out the two-line table (with the odd numbers too) first.

Now try $8 \; 6 \; 2 \; 4$. And then $6 \; 2 \; 4 \; 8$. What do you notice about these three sets of numbers, and the knots they represent?

What about $4 \; 6 \; 8 \; 2$?

In Conclusion

So, now you know that even knots can be named mathematically. You might also be interested to know that the symmetries of knots can be used to distinguish some from others, and in addition can help to determine whether a knot is invertible. If you're keen to try this for yourself, have a go at The Invertible Trefoil .

For a different, but related, challenge you might like to look at the problems Twisting and Turning and More Twisting and Turning which introduce you to the idea of tangles.